Определение площадей плоских фигур

Площадь плоской фигуры, ограниченной непрерывной кривой, уравнение которой в прямоугольных координатах имеет вид y=f(x), осью Ох и двумя прямыми х=а и х=b (a<b) находится по формуле:

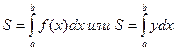
Отрезок [a;b] следует разделить на части, в каждой из которых функция f(x) сохраняет один и тот же знак. При этом следует соблюдать такое правило знаков: площади, находящиеся над осью Ох, берутся со знаком плюс, а площади, расположенные под осью Ох, со знаком минус.

Если площадь ограничена двумя непрерывными кривыми, уравнения которых в прямоугольных координатах 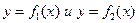, причем всюду на отрезке [a;b] 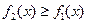и двумя прямыми х=а и х=b, то площадь определяется по формуле:

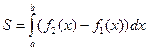и в этом случае надо соблюдать указанное правило знаков.

Примеры.

Найти площадь, ограниченную осью Ох и параболами:

1)

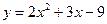
Решение:

Найдем вершину параболы.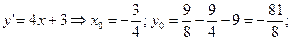

Найдем корни параболы: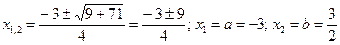

Т.к. фигура находится под осью Ох, то перед определенным интегралом ставим знак минус при определении площади фигуры:

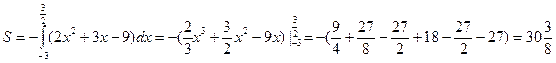
2)

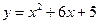
Решение:

Найдем вершину параболы.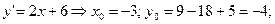

Найдем корни параболы: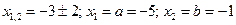

Т.к. фигура находится под осью Ох, то перед определенным интегралом

ставим знак минус при определении площади фигуры:

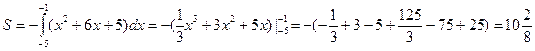
Лекция 12