Основные свойства неопределенного интеграла

Следующие два свойства непосредственно вытекают из определения.

1. Производная от неопределенного интеграла равна подынтегральной функции, а дифференциал от неопределенного интеграла равен подынтегральному выражению:

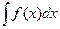( )′= f(x) (1.2)

d( 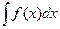)= f(x)dx (1.3)

Благодаря этому свойству правильность интегрирования проверяется дифференцированием. Например, 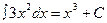, так как

(x³ +C)′=( x³)′=3x²=f(x).

2. Неопределенный интеграл от дифференциала некоторой функции F(x) равен сумме этой функции и произвольной постоянной С.

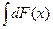= F(x)+C (1.4)

3. Постоянный множитель можно выносить за знак интеграла:

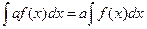(1.5)

где 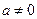- постоянный множитель.

4. Неопределенный интеграл от алгебраической суммы конечного числа непрерывных функций равен алгебраической сумме интегралов от слагаемых функций:

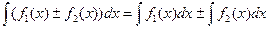(1.6)

5. Инвариантность (неизменность) формулы неопределенного интеграла.

Теорема. Если 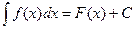, то и 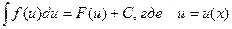- произвольная функция, имеющая непрерывную производную, х – независимая переменная.

Таким образом, формула неопределенного интеграла остается справедливой независимо от того, является ли переменная интегрирования независимой переменной или любой функцией от нее, имеющей непрерывную производную.

Например, заменяя в формуле 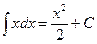х на u, получаем 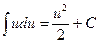. В частности, , .

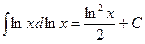Таблица основных неопределенных интегралов

Так как интегрирование есть действие обратное дифференцированию, можно получить таблицу основных интегралов путем обращения соответствующих формул дифференциального исчисления (из таблицы дифференциалов) и использования свойств неопределенного интеграла, например: .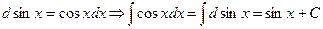

Интегралы в приводимой ниже таблице, называются табличными.

В таблице основных интегралов переменная интегрирования x может быть как независимой переменной, так и функцией от независимой переменной.

Таблица основных интегралов

1. ;

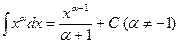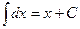
2.

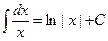
3.

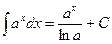
4.

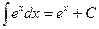
5. ;

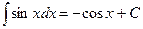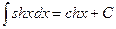
6. ;

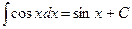7.

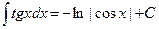
8.

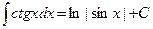
9. ;

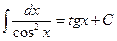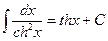
10. ;

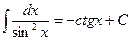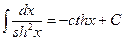
11.

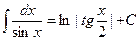
12.

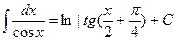
13.

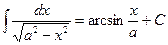
14.

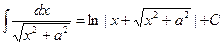
15.

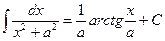
16. ;

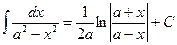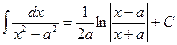
17.

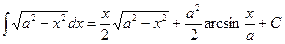
18.

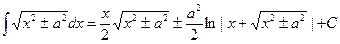
Рекурсивная формула:

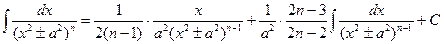
Формула интегрирования иррациональностей следующего вида:

Лекция 2