Распределение Ферми - Дирака

Напомним, что с функцией распределения мы столкнулись впервые при описании распределения молекул газа по скоростям, которое описывалось функцией распределения Максвелла 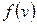. Эта функция дает плотность вероятности того, что у произвольно взятой молекулы скорость окажется равной заданному значению. Соответственно говорят о распределении Максвелла.

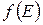Для совокупности одинаковых частиц, участвующих в тепловом движении и находящихся в потенциальном поле сил, справедлива функция распределения Больцмана. Говорят, что такие частицы подчиняются распределению Больцмана. В случае дискретного набора разрешенных значений функция распределения дает вероятность того, что состояние с энергией 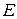занято.

Для совокупности электронов металла при Т = 0 функция распределения должна быть равна единице для значений энергии, меньших , и нулю для остальных значений. Следовательно, ее график имеет вид показанный на рисунке 38.4.

При Т ≠ 0 электроны с уровней, расположенных вблизи переходят на более высокие уровни. Вероятность заполнения становится равной половине, поскольку количество электронов, перешедших на более высокие уровни равно количеству вакантных мест оставленных ими. График функции распределения должен иметь вид, приблизительно показанный на рисунке 38.5.

Теоретический вид функции распределения электронов по состояниям с различной энергией был установлен в работах Ферми и Дирака:

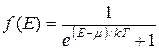(38.25)

Формула (38.25) называется функцией распределения Ферми - Дирака. Параметр m в (38.25) есть химический потенциал.

Частицы, поведение которых описывается (38.25) называются фермионами. Фермионы - это частицы с полуцелым спином. Основное их свойство заключается в том, что на них распространяется действие принципа запрета Паули.

Параметр m в (38.25) в физике твердого тела обычно обозначают и называют уровнем Ферми. Положение уровня Ферми (значение энергии Ферми, соответствующей этому уровню) зависит от температуры, и при Т = 0 совпадет с .

Функция распределения Ферми - Дирака записывается с использованием обозначения в виде:

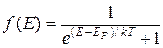(38.26)

Функция (15) действительно соответствует поведению электронов:

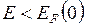при Т = 0 = 1, если ;

, если .

От метим, что независимо от температуры .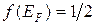

Значение параметра в функции распределения в принципе можно найти из условия, что полное число электронов, заполняющих уровни, должно равняться числу свободных электронов в кристалле – nV.

По определению функции плотности состояний, количество состояний 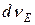в интервале энергий от от Е до

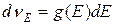(38.27)

Умножив это значение на вероятность заполнения уровня 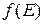, найдем среднее число электронов, находящихся в этих состояниях:

(38.28)

Интеграл от (38.28) по всем энергиям должен быть равен полному числу свободных электронов в кристалле:

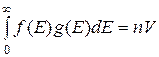(38.29)

Оказалось, что интеграл (38.29) в общем случае не берется. Можно найти его приближенное значение при условии 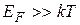. И тогда получается

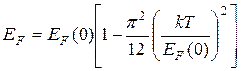(38.30)

Из (38.30) следует, что, что 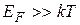E_F зависит от температуры при низких температурах очень слабо. Но сам факт зависимости имеет принципиальное значение.

Для больших энергий, когда 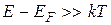, иными словами в области "хвоста" функции распределения, единицей в ее знаменателе можно пренебречь и функция Ферми - Дирака переходит в распределение Больцмана

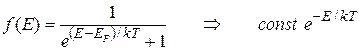(38.30)

Это означает, что электроны с такими энергиями описываются классическим распределением, и квантовые особенности их поведения становятся несущественны. Таким образом, поведение электронного газа кристалла сильно зависит от соотношения между температурой кристалла и температурой Ферми: .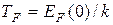

1. Если 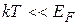электроны описываются функцией распределения Ферми – Дирака и электронный газ называется вырожденным. У металлов температура Ферми составляет десятки тысяч кельвинов, поэтому электронный газ, как правило вырожденный

2. 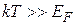Для описания электронного газа можно использовать классическую статистику, то есть функцию распределения Больцмана. Электронный газ называется невырожденным. Поскольку значение энергии Ферми ~ 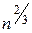, то в полупроводниках, где концентрация свободных электронов на несколько порядков ниже, чем в металлах, оказывается намного ниже, и электронный газ оказывается невырожденным.