Основные результаты решения уравнения Шредингера для электронов в кристалле в приближении почти свободных электронов

<7980 81 82 83 84 85 >

Уравнение Шредингера в приближении почти свободных электронов решается методами теории возмущений, и в качестве нулевого приближения используются волновые функции свободных электронов, а периодическая потенциальная энергия U( 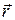) рассматривается как возмущение. В первом приближении теории возмущений спектр энергии электронов смещается вниз на величину средней потенциальной энергии <U>, и это соответствует тому факту, что кристалл представляет для для электронов потенциальную яму.

Во втором приближении для большинства состояний поправка к энергии практически равна нулю. Главное воздействие слабый периодический потенциал оказывает лишь на те уровни свободного электрона, волновые векторы которых близки к векторам, допускающим брэгговское отражение.

Распространение волн в средах с периодически изменяющимися свойствами сопровождается появлением качественных особенностей, наиболее заметных в тех случаях, когда длина волны становится сравнимой с характерным пространственным периодом изменения свойств системы. Не смотря на физические различия, волновые процессы в различной природы в периодических системах описываются похожими уравнениями, и сходными оказываются особенности распространения волн.

Типичными средами с периодически изменяющимися свойствами являются кристаллы. При распространении в кристалле электромагнитных волн имеет место брэгговское отражение, наблюдаемое, например, для электромагнитных волн при выполнении закона Вульфа – Брэгга.

Рисунок 4.

Напомним. Представим себе кристаллическую решетку. Проведем через узлы кристаллической решетки параллельные равностоящие друг от друга плоскости, которые будем называть атомными слоями. Две системы атомных слоев (сплошные и пунктирные линии показаны на рисунке 4) Суммарное действие атомов, лежащих в одном слое, можно представить в виде плоской волны, отра зившееся от усеянной атомами поверхности по обычным законам отражения. Плоские вторичные волны, отразившееся от разных атомных слоев, являются когерентными и будут интерферировать. При этом, как в случае решетки, вторичные волны будут практически погашать друг друга во всех направлениях, кроме тех, для которых разность хода для волн, отразившихся от соседних атомных слоев, является кратной длине волны используемого излучения λ.

Как следует из рисунка 4, разность хода таких двух волн равна 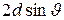, где d – расстояние между рассматриваемыми атомными слоями, угол 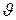- угол скольжения. Направление, в котором получаются дифракционные максимумы, определяется условием

Это соотношение называется формулой Вульфа-Брэгга.

Условие брэгговского отражения для одномерного кристалла: 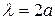. При его выполнении бегущая волна эффективно отражается от периодических неоднородностей среды, и ее энергия передается волне, бегущей в противоположном направлении. Встречная волна в свою очередь переотражается, возвращая часть энергии прямой волне. Волны оказываются сильно связанными друг с другом. В этом случае на дисперсионной кривой (дисперсионной кривой называется зависимость, связывающая частоту воны и ее волновой вектор ) появляется область запрещенных частот 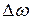- рисунок 39.2. Волны с частотами из этой области в кристалле не распространяются, испытывая сильное затухание.

Брэгговское отражение имеет место и для электронных волн в кристалле. В рамках теории Зоммерфельда, т.е. в приближении свободных электронов, волновые функции электронов имеют вид плоских волн. При распространении таких волн в кристалле они испытывают сильное отражение при выполнении условия Брэгга, и это, в конечном итоге, приводит к появлению в дисперсионном законе электронов энергетической щели.

Рассмотрим сначала простейшую модель кристалла в виде линейной цепочки атомов на расстоянии а друг от друга. Для полностью свободных электронов в области низких значений энергий зависимость энергии от волнового вектора имеет вид и показана на рисунке 39.3.

Слабо связанные электроны испытывают брэгговское отражение при выполнении условия Вульфа-Брэгга 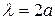. В одномерном случае можно представить в виде:

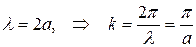
В общем случае отражения наступают при выполнении условия:

k = ± n p /а, (39.3)

Первые отражения (и соответственно энергетическая щель) имеют место при k = ± p /а. Эти отражения получаются, когда электронная волна от данного атома линейной цепочки интерферирует с волной от его ближайших соседей. Разность фаз между этими волнами равна как раз ±2p, и можно сказать, что волна, бегущая в одном направлении, испытав брэгговское отражение, распространяется затем в противоположном направлении. Каждое последующее отражение вновь обращает направление распространения волны. Единственной не зависимой от времени картиной, отвечающей такой ситуации, является картина образования стоячих волн.

При выполнении k = ± p /а волновые функции электрона уже не являются бегущими волнами вида ехр(ip x/a) и ехр( - ip x /a). Из этих бегущих волн можно сформировать две различные стоячие волны - четную и нечетную, которые (без учета условия нормировки) имеют вид:

= ехр(ipx/a) + ехр(-ipx/a) = 2cos(p x/a); = ехр(ipx/a) - ехр(-ipx/a) = 2sin(px/a).

(39.4)

Представленные две стоячие волны отвечают группировке электронов в различных по отношению к ионам областях пространства и, следовательно, соответствующие электроны имеют различные значения потенциальной энергии. Это обстоятельство и является причиной существования энергетической щели.

Функция описывает скопление отрицательного заряда вблизи положительных ионов.

Функция 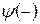описывает такое распределение электронов, при котором они располагаются преимущественно в областях, соответствующих серединам расстояний между ионами, т.е. вне ионных остовов.

Средние значения потенциальной энергии для электронов, локализованных в разных местах по отношению к периодическому потенциалу отличаются на некоторую величину Е_v, а значит, существует энергетическая щель такой ширины между энергиями электронов в состояниях с одинаковыми волновыми векторами k = ± p /а. На графике дисперсионного закона для электронных волн существование энергетической щели отражается в виде, показанном на рисунке 39.4. Волновая функция 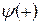соответствует точкам А, а 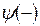- точкам В.

Зависимость энергии от волнового вектора при учете поля решетки имеет вид: рисунок 39.5.

Каждая разрешенная зона состоит из большого количества близкорасположенных уровней, число которых равняется количеству атомов в образце кристалла.

Области k–пространства внутри, которых энергия электронов изменяется квазинепрерывно, называютсязонами Бриллюэна. На границах зон Бриллюэна энергия терпит разрыв. Для трехмерных кристаллов границами зон в k - пространстве являются замкнутые многогранные поверхности, заключенные одна в другой.

В силу периодической зависимости энергии от волнового вектора, можно ограничиться рассмотрением только первой зоны Бриллюэна. В этом случае зависимость Е(k) оказывается многозначной функцией волнового вектора, но в пределах каждой зоны функция однозначна. Такое представление энергетических зон называют схемой приведенных зон. Схема приведенных зон показана на рисунке 39.6.

Отличительной особенностью одномерного случая, для которого структура энергетических зон показана на рисунках 39.5 и 39.6, является то, что зоны разрешенных значений энергии всегда разделены запрещенными зонами. В двумерном и трехмерном случаях это не всегда имеет место.

Изоэнергетическая поверхность в k - пространстве для энергии E_F называется поверхностью Ферми. Для свободных электронов оная является сферой, а в действительности для электронов кристалла зависит от конкретных свойств кристалла и часто имеет весьма причудливый вид. Форма поверхности определяет характер движения электронов с энергией, близкой к E_F, а именно эти электроны участвуют в переносе заряда, т.е. создании электрического тока

Ширина разрешенных и запрещенных зон не зависит от размеров кристалла и имеет величину около нескольких эВ. Соответственно расстояние между разрешенными уровнями ≈ 10^-23 эВ.

Существование энергетических зон позволяет с единой точки зрения объяснить существование металлов диэлектриков и полупроводников.

<7980 81 82 83 84 85 >

Дата добавления: 2021-01-11; просмотров: 323;