Теория теплоемкости кристаллов Дебая
В реальном критсталле все атоомы связаны друг с другом и смещение из положения равновесия одного вызывает смещение соседних. В результате по кристаллу распространяется волна. На границе кристалла волна отражается, накладывается на падающую, и в результате возникает стоячая волна, аналогичная волне, распространяющейся в струне. Стоячие волны в кристалле, как и в струне гармоники, образуются не на всех частотах, а только на выделенных, набор которых определяется размерами кристалла и скоростью распространения волн в кристалле. Стоячие волны в кристалле представляют собой нормальные колебания кристалла. Обращает на себя внимание аналогия волн, распространяющихся в кристалле, и электромагнитных волн, существующих в полости с отражающими стенками.
Напомним, что количество стоячих волн, с частотами в интервале от 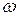 до
до 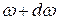 , в расчете на единицу объема, в котором они распространяются, определяется соотношением:
, в расчете на единицу объема, в котором они распространяются, определяется соотношением:
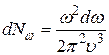 . (31.17)
. (31.17)
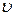 - фазовая скорость распространения волн.
- фазовая скорость распространения волн.
В кристалле в данном направлении могут распространяться независимо три волны – две поперечных, поляризованных во взаимно перпендикулярных плоскостях и одна продольная. Для упрощения рассуждений предположим, что скорости продольных 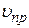 и поперечных
и поперечных  совпадают,
совпадают,  . Тогда
. Тогда
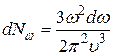 . (37.15)
. (37.15)
 Дискретность структуры кристалла приводит к тому, что частоты нормальных колебаний ограничены сверху некоторой частотой
Дискретность структуры кристалла приводит к тому, что частоты нормальных колебаний ограничены сверху некоторой частотой  . Действительно в бесконечной цепочке атомов формально можно представить волну с большей частотой (на рисунке 37.9 она показана темно зеленой). Однако атомов, способных осуществить такие смещения нет, и такой волны реально не может быть, поскольку у нее нет материального носителя.
. Действительно в бесконечной цепочке атомов формально можно представить волну с большей частотой (на рисунке 37.9 она показана темно зеленой). Однако атомов, способных осуществить такие смещения нет, и такой волны реально не может быть, поскольку у нее нет материального носителя.
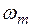 можно найти из условия, что полное число нормальных колебаний должно быть равно числу степеней свободы колебательной системы. Есди концентрация атомов в кристалле равна
можно найти из условия, что полное число нормальных колебаний должно быть равно числу степеней свободы колебательной системы. Есди концентрация атомов в кристалле равна 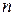 , то для единицы объема кристалла число степеней свободы должно быть равно
, то для единицы объема кристалла число степеней свободы должно быть равно  . Поэтому
. Поэтому
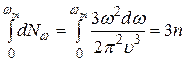 . (37.16)
. (37.16)
Интегрируя, находим:
 . (37.17)
. (37.17)
Подставив это значение  в (37.15), для
в (37.15), для 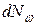 получим
получим
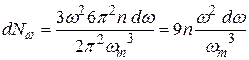 . (31.18)
. (31.18)
Для нормальных колебаний энергия системы равна сумме энергий нормальных колебаний. Поэтому внутреннюю энергию единицы объема кристалла можно рассчитать, умножив среднюю энергию 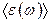 колебания частоты
колебания частоты 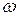 на количество колебаний в интервале от
на количество колебаний в интервале от 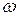 до
до 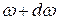 -
- 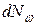 , и проинтегрировав полученное выражение в интервале от нуля до
, и проинтегрировав полученное выражение в интервале от нуля до 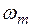 :
:
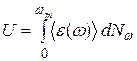 . (37.19)
. (37.19)
Сравним подходы в теории Эйнштейна и Дебая. Представив кристалл в виде системы независимых одинаковых осцилляторов, Эйнштейн рассчитывал внутреннюю энергию простым умноженикем:  . В теории Дебая расчет гораздо ближе к действительности, и получается более точное, но и более сложное соотношение (37.19).
. В теории Дебая расчет гораздо ближе к действительности, и получается более точное, но и более сложное соотношение (37.19).
Подставим в (37.19) выражения для 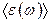 и
и 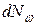 :
:
 . (37.20)
. (37.20)
Проведем анализ для области высоких и низких температур. Величину 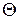 , определяемую из условия
, определяемую из условия
 , (37.21)
, (37.21)
называют температурой Дебая. Эта температура разграничивает область высоких температур, когда дискретностью изменения энергии можно пренебречь, и область низких температур, в которой определяющем фактором является как раз допустимость изменения энергии только на величину  .
.
В области высоких температур, т.е.  ,
, 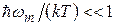 и можно положить, что
и можно положить, что  . Тогда
. Тогда
 . (37.22)
. (37.22)
Теплоемкость единицы объема кристалла
 . (37.23)
. (37.23)
Положив  (числу Авогадро), для молярной теплоемкости получаем значение
(числу Авогадро), для молярной теплоемкости получаем значение  , в соответствии с законом Дюлонга и Пти.
, в соответствии с законом Дюлонга и Пти.
В области низких температур, т.е. 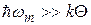 , дифференцируя (37.20), находим:
, дифференцируя (37.20), находим:
 . (37.24)
. (37.24)
Обозначим  . Тогда
. Тогда  . Подставим эти значения в (37.24):
. Подставим эти значения в (37.24):
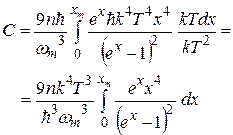 . (37.25)
. (37.25)
Условие 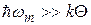 означает, что
означает, что
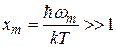 . (37.26)
. (37.26)
Поэтому верхний предел интеграла можно положить равным бесконечности. Тогда весь интеграл можно считать равным некоторому числу, и из (37.25) следует, что
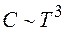 . (37.26)
. (37.26)
в соответствии с экспериментальными данными. В связи с этим температурную зависимость теплоемкости в области низких температур принято называть законом  Дебая.
Дебая.
 Для простых кристаллов, например металлов алюминий, медь и др. точные расчеты по формулам, полученным Дебаем дают превосходное соответствие экспериментальным данным. К кристаллам со сложной структурой формулы Дебая непосредственно неприменимы. Это обусловлено тем, что у сложных кристаллов спектр колебаний также оказывается очень сложным. В рассмотренном нами случае каждому значению волнового вектора соответствовало три значения частоты (мы положили их равными…). Если число атомов в элементарной ячейке равно
Для простых кристаллов, например металлов алюминий, медь и др. точные расчеты по формулам, полученным Дебаем дают превосходное соответствие экспериментальным данным. К кристаллам со сложной структурой формулы Дебая непосредственно неприменимы. Это обусловлено тем, что у сложных кристаллов спектр колебаний также оказывается очень сложным. В рассмотренном нами случае каждому значению волнового вектора соответствовало три значения частоты (мы положили их равными…). Если число атомов в элементарной ячейке равно 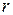 , то то каждому значению волнового вектора соответствуют
, то то каждому значению волнового вектора соответствуют 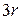 различных частот, т.е. частота оказывается многозначной функцией волнового вектора.
различных частот, т.е. частота оказывается многозначной функцией волнового вектора.
Даже в простейшем случае одномерного кристалла с двумя атомами в элементарной ячейке зависимость частоты колебания от волнового вектора  , которую называют дисперсионным законом, имеет вид показанный примерно на рисунке 37.10. В соответствии с количеством атомов (кристалл одномерный – число ветвей равно
, которую называют дисперсионным законом, имеет вид показанный примерно на рисунке 37.10. В соответствии с количеством атомов (кристалл одномерный – число ветвей равно 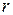 ) зависимость имеет две ветви, одну из которых называют акустической, а вторую – оптической. В колебаниях акустической ветви элементарные ячейки движутся как целое. В колебаниях акустической ветви атомы смещаются друг отьносительно друга в элементарной ячейке и она, как правило приобретает дипольный электрический момент. В силу этого колебания оптической ветви могут интенсивно взаимодействовать с электромагнитными, чем и объясняется название ветви.
) зависимость имеет две ветви, одну из которых называют акустической, а вторую – оптической. В колебаниях акустической ветви элементарные ячейки движутся как целое. В колебаниях акустической ветви атомы смещаются друг отьносительно друга в элементарной ячейке и она, как правило приобретает дипольный электрический момент. В силу этого колебания оптической ветви могут интенсивно взаимодействовать с электромагнитными, чем и объясняется название ветви.
Понятие о фононах
С представлением о стоячих волнах, существующих в некотором объеме мы столкнулись дважды – один раз при рассмотрении плотности энергии электро-магнитных волн в полости, а второй – при рассмотрении теории Дебая. В случае электро-магнитных волн ситуацию в полости можно представлять как газ фотонов. Аналогичным образом колебания кристаллической решетки можно представить как газ особых частиц, которые могут существовать и распространяться в пределах кристалла. Действительно, энергия нормального колебания с частотой  –
–  – складывается из порций (квантов) величиной
– складывается из порций (квантов) величиной
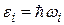 . (37.27)
. (37.27)
– также как и для фотонов. Отличие только в существовании нулевых квантовых колебаний. Порции (кванты) энергии колебаний кристаллической решетки называют фононами. В силу того, что для существования фононов необходимо наличие среды, кристалла, фононы называют квазичастицами.
Во многих случаях (рассеяние рентгеновских лучей, комбинационное рассеяние света, расеяние ней тронов и др.) при описании процессов в кристалле удобно рассматривать колебания в ристалле, как газ фононов, каждый из которых обладает кроме энергии (37.27) квазиимпульсом
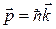 , (37.28)
, (37.28)
где 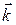 – волновой вектор номального колебания.
– волновой вектор номального колебания.
Среднюю энергию колебания частоты  молжно представить, с одно стороны, как произведение
молжно представить, с одно стороны, как произведение 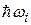 на среднее число фононов с
на среднее число фононов с 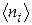 частотой
частотой  , а с другой стороны в соответствии с формулой (37.01). Поэтому справедливо соотношение
, а с другой стороны в соответствии с формулой (37.01). Поэтому справедливо соотношение
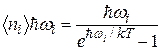 , (37.29)
, (37.29)
и среднее число фононов определяется формулой:
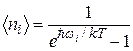 . (37.30)
. (37.30)
С ростом температуры 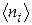 , а значит и количество одинаковых фононов, неограниченно возрастает. Это указывает на то, что принципу Паули фононы не подчиняются. Это утверждение справедливо и для фотонов!
, а значит и количество одинаковых фононов, неограниченно возрастает. Это указывает на то, что принципу Паули фононы не подчиняются. Это утверждение справедливо и для фотонов!
Формула (37.30) является частным случаем распределения Бозе-Эйнштейна, которое описывает поведение частиц с целым спином:
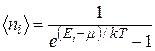 . (37.31)
. (37.31)
Параметр распределения 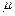 называется химическим потенциалом, и определяется из условия
называется химическим потенциалом, и определяется из условия
 ,
,
где  - полное число частиц в системе.
- полное число частиц в системе.
Для систем с переменным числом частиц, таких как фотоны и фононы, химический потенциал равен нулю.
Частицы, подчиняющиеся распределению Бозе-Эйнштейна (37.31) назы-вают бозонами. Важной особенностью всех бозонов является тот факт, что вероятность возникновения бозона в состоянии, где уже имеется  частиц, пропорциональна этому числу. Именно эта особенность
частиц, пропорциональна этому числу. Именно эта особенность
Дата добавления: 2021-01-11; просмотров: 589;











