Для электронов в кристалле

Приближенное решение уравнения Шредингера для электрона в периодическом поле проводится с использованием теории возмуще­ний (метода последовательных приближений), применимого в тех случаях, когда некоторое воздействие на систему (возмущение) может считаться малым. При этом сначала находится более простое решение для «невозмущенной» системы, а затем с помощью этого решения вычисляются поправки, вносимые возмущением. «Подправленное» решение используется для нахождения новых поправок (второго по­рядка). Такая процедура повторяется до достижения необходимой точности, когда новые поправки становятся пренебрежимо малыми. Если возмущение действительно мало, то вычисляемые поправки быстро убывают, и в итоге можно ограничиться поправками невысо­ких порядков.

Существуют два приближения при решении задачи о движении электрона в периодическом поле, отличающиеся выбором нулевого приближения.

В приближении почти свободных электронов считается, что кинетическая энергия электрона значительно больше пространствен­ных изменений потенциальной энергии U( 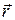) в периодическом поле ионов решетки, и влияние периодиче­ского потенциала кристаллической решетки можно рассматривать как малое возмущение движения свободного электрона. Однако, согласно выводам квантовой механики, средняя кинетическая энергия элек­трона в квантовомеханической системе (атоме, молекуле, кристалле) должна быть порядка колебаний его потенциальной энергии. Поэтому количественная применимость выводов, получаемых в этом прибли­жении, представляется весьма сомнительной.

Тем не менее, во многих случаях приближение почти свободных электронов дает удивительно точные результаты, в частности, для металлов 1 - 4 групп периодиче­ской таблицы. Можно указать две причины, по которым сильное взаимодействие электронов проводимости между собой и с положи­тельными ионами приводит к суммарному эффекту, описываемому слабым потенциалом.

1. Взаимодействие между электронами и ионами наиболее сильно на малых расстояниях. Однако принцип Паули запрещает электронам проводимости появляться вблизи ионов, поскольку эта область уже занята электронами ионного остова.

2. В той области, которая разрешена для электронов проводимо­сти, они, благодаря своей подвижности, дополнительно уменьшают суммарный потенциал, действующий на отдельный электрон за счет экранировки поля положительных ионов.

В приближении сильно связанных электронов считается, что состояние электрона в кристалле мало отличается от состояния в изо­лированном атоме. Это приближение вполне оправдано для электро­нов глубоких энергетических уровней атомов, но для электронов, перемещающихся по кристаллу при протекании электрического тока, их сильная связь с атомами представляется маловероятной.

Ни одно из указанных приближений не позволяет производить количественных расчетов энергетического спектра и волновых функ­ций электронов проводимости в конкретных кристаллах. Но сущест­венно, что они дают хорошую иллюстрацию к общим выводам о дви­жении электрона в периодическом поле.