Когда границы рудного тела не известны

В некоторых случаях границы рудного тела заранее не известны. Поэтому они должны быть определены из доступной информации, например - данных опробования скважин. Эта неопределенность знаний о геометрии рудного тела приводит ко второму источнику ошибки, называемой геометрической ошибкой, которая должна быть добавлена к ошибке, описанной ранее.

Рис 10.5. Расположение минерализованных и породных блоков на участке. Скважины расположены в центрах соответствующих блоков.

На Рис. 10.5 изображен регион, содержащий 48 скважин. Семнадцать из них попадают в рудное тело (соответствующие блоки заштрихованы), остальные нет. Простейший путь определить размеры рудного тела – это объединить все квадраты сетки с положительными результатами.

Матерон (1971 a и b) получил формулу для отношения геометрической ошибки к квадрату минерализованной области A:

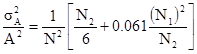[10.21]

где N – количество положительных (минерализованных) проб (здесь 17). Параметры N₁ и N₂ находятся подсчетом количества сторон квадратов сетки по вертикали и горизонтали. Чтобы быть более точным, N₁ и N₂ вычислены делением общего количества квадратов сетки в каждом направлении на 2. Обратите внимание, что N₁ должно быть больше или равно N₂. В примере – 12 горизонтальных сторон и 10 вертикальных сторон. Поэтому при N₁=6 и N₂=5, получаем

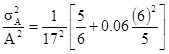[10.22]

Результат равен (6.6%)², что не является очень большим.

Обратите внимание, что при вычислении N₁ и N₂ все выступы и впадины на границах зоны должны быть подсчитаны, включая периметр внутренних скважин (блоков). Это проиллюстрировано на Рис. 10.6. В итоге геометрическая ошибка должна быть введена в дисперсию оценивания. При выполнении этого требуется некоторая осторожность. Для большей информации смотрите примеры, приведенные Journel и Huijbregts (1978) на стр. 428-438. Похожая формула существует и для трехмерного случая.

Рис 10.6. Расположение минерализованных и породных блоков (скважин)

На Рис. 10.6 изображена конфигурация с пустой зоной в центре рудного тела. Это обстоятельство затрудняет вычисление N₁ и N₂. Сначала рассмотрим вертикальное направление, общее количество сторон квадратов сетки по внешней границе 16, а внутри 6 сторон квадратов, что дает в итоге 22. Аналогично - в горизонтальном направлении, общий периметр равен 26 (20+6). Это означает, что N₁ равно 13 и N₂ равно 11. Остальные вычисления производятся так же как и раньше.