Дисперсия распространения

Предположим, что мы хотим оценить среднее содержание внутри региона V; т.е. мы хотим вычислить интеграл:

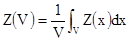[10.1]

Предположим также, что доступной информацией является лишь среднее содержание в маленьком блоке v. Обычно V является извлекаемым блоком или участком, а v – скважиной или пробой другого типа. Поэтому мы должны оценить Z(V) из Z(v), где:

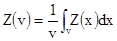[10.2]

Считается нормальным использовать содержание Z(v), как оценку для Z(V). Какая в этом ошибка? Во-первых, если Z(x) удовлетворяет стационарной или внутренней гипотезе, то Z(v) - несмещенная оценка Z(V). Нам нужно вычислить дисперсию распространения содержания v в V. Иногда это обозначается 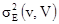или, для краткости, - .

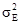Концептуально - это просто дисперсия оценивания Z(V) через Z(v). В геостатистике выражение " дисперсия распространения " обычно используется для случая, когда блок оценивается по содержанию пробы в его центре. В общем случае выражение "дисперсия распространения" используется для более сложных ситуаций, где в вычислениях участвует несколько проб. Теоретически значение дисперсии распространения получается из:

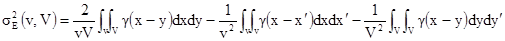[10.3]

Поэтому

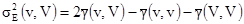[10.4]

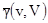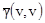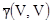где , и - средние значения вариограмм, когда конечные точки вектора h независимо движутся внутри V и v соответственно.

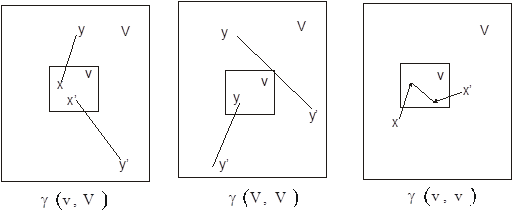
Рис 10.1. Смысл среднего в терминах вариограммы

Формула [10.4] подходит для любых форм v и V. В особенности, когда v не размещается внутри V. Факторы, действующие на дисперсию распространения:

регулярность переменной (через g),

геометрия V,

геометрия v,

расположение v относительно V.

Эту формулу можно переписать в виде:

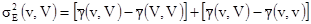[10.5]

Это преобразование делает понятным, что дисперсия уменьшается, когда:

проба v лучше представляет оцениваемый регион V. В предельном случае v=V, .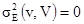

вариограмма более регулярна, т.е. переменная более непрерывна.

Другое понятное и не менее важное свойство дисперсии распространения – она использует вариограмму и геометрию оцениваемой области, но не действительные значения проб. Это свойство также характерно для дисперсии и весов кригинга.