Прямая композиция выражений

В первом случае мы предполагаем, что пробы расположены по регулярной или почти по регулярной сетке. Чтобы оценить общий тоннаж руды, надо умножить площадь региона на среднюю мощность пласта или жилы (здесь среднее обозначает среднеарифметическое). Расчеты, включая кригинг, использующие большое количество проб, расположенных по регулярной сетке, показали, что весовые факторы проб очень близки к 1/N, где N – количество проб. Поэтому наша оценка равна:

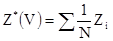[10.6]

Соответствующая дисперсия оценивания –

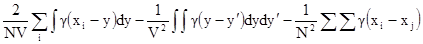[10.7]

Если N большое, то эта формула становится очень громоздкой. Поэтому мы аппроксимируем ее, предполагая, что сумма ковариаций между ошибками распространения равна нулю. На Рис. 10.2 изображены N квадратов с пробами в центрах. Пусть Z(v_i) будет действительным, но неизвестным средним i-го квадрата.

Рис 10.2. Регулярная сеть опробования

Так как среднее всей области является просто средним маленьких квадратов, то ошибка, полученная при использовании среднего проб, как оценки области, равна:

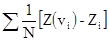[10.8]

Таким образом, это будет среднее частичных ошибок. Чтобы упростить вычисления, предположим, что сумма ковариаций между ними равна нулю. Проверка, сделанная Давидом (1973, 1977, стр. 201), показала, что это достаточно хорошая аппроксимация. Отсюда получаем дисперсия оценивания

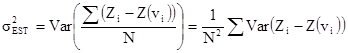[10.9]

Теперь 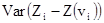является дисперсией распространения центрального значения пробы до всего квадрата v_i. Так как все квадраты имеют одинаковый размер, то

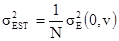[10.10]

Вышеописанное представляет собой простой способ оценки общих запасов и дисперсии оценивания в терминах вариограммной функции. (Обратите внимание: этот же метод можно применить, когда не все блоки v_i одинакового размера. Смотрите для деталий Journel и Huijbregts (1978) стр 415-417).

Этот метод основан на прямой композиции. Он верен только в том случае, когда блоки примерно квадраты. Если отношение длины блока к ширине больше 3:1, то нужно использовать композицию линией и сечением, которые описываются в следующем параграфе. Когда решается вопрос, какой принцип аппроксимации использовать, нужно учитывать анизотропию вариограммной модели. Отношение длины блока к его ширине следует вычислять в единицах зоны влияния вариограммы, а не в единицах расстояния. Например, если пробы расположены по действительно квадратной сети (Рис. 10.2), но вариограмма имеет отношение анизотропии 2:1, то конфигурация проб после учета анизотропии растянется как показано на Рис. 10.3.

Рис 10.3. Сеть опробования после учета анизотропии