Вывод распределения по Максвеллу

Получим теперь формулу распределения так, как это делал сам Джеймс Клерк Максвелл.

Рассмотрим пространство скоростных точек (каждую скорость молекулы представляем как точку (скоростную точку) в системе координат 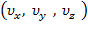встационарном состоянии газа. Выберем бесконечно малый элемент объема 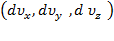.Так как газ стационарный, количество скоростных точек в 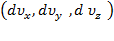остается неизменным с течением времени. Пространство скоростей изотропно, поэтому функции плотности вероятности для всех направлений одинаковы.

, , .

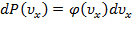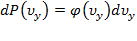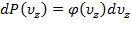Максвелл предположил, что распределения скоростей по направлениям статистически независимы, то есть компонента 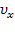скорости молекулы не зависит от 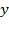и –компонент.

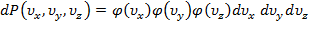
–фактическая вероятность нахождения скоростной точки в объём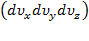е ,где 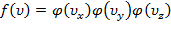.Прологарифмируем последнее равенство:

.

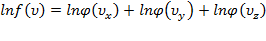Дифференцируя полученное выражение по компоненте скорости 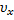, получим:

,

,

.

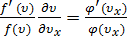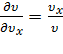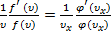Правая часть не зависит от 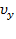и 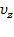, значит и левая от 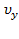и 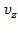не зависит. Однако, 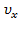и 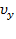равноправны, следовательно, левая часть не зависит также и от 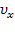. Значит, данное выражение может лишь равняться некоторой константе.

,

,

.

.

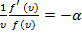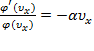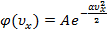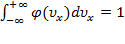Следовательно, .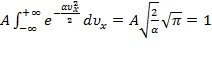

Отсюда: .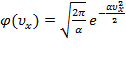

Теперь нужно сделать принципиальный шаг – ввести температуру. Кинетическое определение температуры (как меры средней кинетической энергии движения молекул):

,

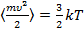где 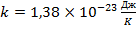–постоянная Больцмана; 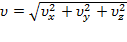. Ввиду равноправия всех направлений: .

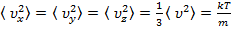Чтобы найти среднее значение 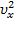, проинтегрируем её вместе с функцией плотности вероятности от минус до плюс бесконечности:

.

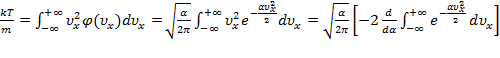Отсюда найдём : .

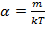Функция распределения плотности вероятности для 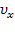(аналогично для ; ): .

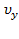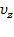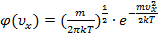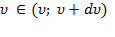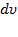Теперь рассмотрим распределение по величине скорости. Вернемся в пространство скоростных точек. Все точки с модулем скорости лежат в шаровом слое радиуса и толщины , и 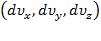–объем этого шарового слоя.

.

.

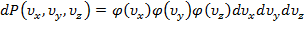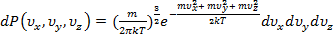Учтём, что: 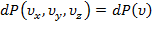; 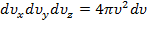, получим:

,

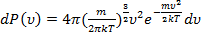где 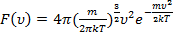.Тогда окончательно получим: .

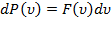Таким образом, мы получили функцию плотности вероятности 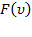, которая и является распределением Максвелла.