Границы применимости

Условия применимости распределения Максвелла:

1. Равновесное состояние системы, состоящей из большого числа частиц.

2. Изотропная система.

3. Классическая система. Это значит, что система должна быть не релятивистской и не квантовой (взаимодействие частиц допускается, но только зависящее от относительного положения частиц).

Относительное число молекул 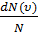, со скоростями, лежащими в интервале от 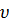до , рассчитывается как площадь заштрихованной полоски на рис. 111. Площадь, которая ограничена кривой распределения и осью абсцисс, равна единице. Это значит, что функция 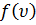удовлетворяет условию нормировки : .

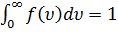Вид функции распределения 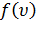(рис. 111):

На рис. 111: 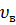– наиболее вероятная скорость молекул, соответствует максимуму кривой; 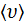–средняя скорость молекул газа; 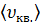– cредняя квадратичная скорость молекул газа.

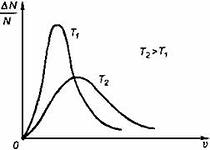Рис. 112. Зависимость функции распределения Максвелла от температуры.

Рис. 111.

С ростом температуры максимум кривой распределения смещается в сторону больших температур (рис. 112).

Хотя уравнение Максвелла дает распределение скоростей, или, другими словами, долю молекул, имеющих специфическую скорость, часто более интересны другие величины, такие как средние скорости частиц. В следующих подразделах мы определим и получим наиболее вероятную скорость, среднюю скорость и среднеквадратичную скорость.

Характерные скорости