Основы механики жидкостей и газов

Предмет гидроаэромеханики

Гидроаэромеханика – раздел механики, посвящённый изучению равновесия и движения жидких и газообразных сред и их взаимодействия между собой и обтекаемыми ими твёрдыми телами.

Движение несжимаемой жидкости изучается в гидродинамике, а газов – в аэродинамике.

Газ и жидкость в гидроаэромеханике

Газ (от греч. chaos – хаос) – агрегатное состояние вещества, в котором его частицы не связаны или слабо связаны силами взаимодействия и движутся свободно, занимая весь предоставленный им объём.

В отличие от твёрдых тел и жидкостей объём газа существенно зависит от давления и температуры.

Жидкость – это агрегатное состояние вещества, промежуточное между твёрдым и газообразным.

Жидкости присущи некоторые черты твёрдого тела (сохраняет свой объём, образует поверхность, обладает определённой прочностью на разрыв) и газа (принимает форму сосуда, в котором находится, может непрерывно переходить в газ); в то же время она обладает рядом только ей присущих особенностей, из которых наиболее характерной является текучесть.

Нормальные жидкости макроскопически однородны и изотропны при отсутствии внешних воздействий. Последнее так же сближает их с газами.

В гидроаэромеханике жидкости и газы рассматривают как сплошную, непрерывную среду, отвлекаясь от их молекулярного строения.

Хотя свойства жидкостей и газов во многом отличаются, в ряде механических явлений их поведение описывается одинаковыми параметрами и идентичными уравнениями.

Предмет гидроаэростатики

Гидростатика – раздел гидроаэромеханики, в котором изучаются равновесие жидкости и воздействие покоящейся жидкости на погруженные в неё тела, жидкость при этом считается практически несжимаемой.

Аэростатика – раздел гидроаэромеханики, в котором изучается равновесие газообразных сред, в основном атмосферы.

При этом необходимо учитывать, что сжимаемость газов во много раз превосходит сжимаемость жидкостей.

Основными законами гидроаэростатики являются закон Паскаля[18] и закон Архимеда[19].

Давление покоящейся жидкости (газа). Закон Паскаля

Закон был установлен экспериментально французским учёным Б.Паскалем в 1648 г.: давление, производимое на покоящуюся жидкость (газ) внешними силами передаётся жидкостью (газом) одинаково во всех направлениях (рис. 86): 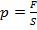, Па, где 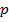– это давление, 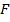– приложеннаясила, 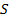– площадь поверхности, на которую действует) сила давления .

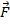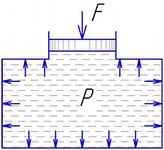Рис. 86.

Это утверждение объясняется подвижностью частиц жидкостей и газов во всех направлениях. Из формулы мы видим, что при увеличении силы воздействия при той же площади сосуда давление на его стенки будет увеличиваться.

Действительно, если в покоящуюся жидкость (газ) поместить небольшую тонкую пластинку, то части жидкости (газа), находящиеся по разные стороны от неё, будут действовать на каждый её элемент 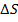с силами 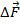, которые независимо от того, как пластинка ориентирована, будут равны по модулю и направлены перпендикулярно площадке 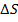, т.к. наличие касательных сил привело бы частицы жидкости в движение (рис. 87).

Рис. 87.

Для сжимаемых жидкостей (газов) закон Паскаля, вообще говоря, несправедлив.

Закон Паскаля неприменим в случае движущейся жидкости (газа), а также в случае, когда жидкость (газ) находится в гравитационном поле; так, известно, что атмосферное и гидростатическое давление уменьшается с высотой.

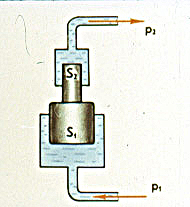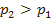Рис.88. Гидравлический мультипликатор предназначен для увеличения давления ( , так как при одинаковой силе давления ).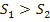

На основе закона Паскаля работают различные гидравлические устройства: тормозные системы, гидравлические прессы и др., например, гидравлический мультипликатор (рис. 88), гидравлический пресс (рис. 89).

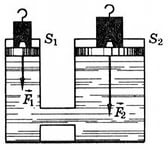Рис. 89.

Гидравлический пресс

Гидравлический пресс– это простейшая гидравлическая машина, предназначенная для создания больших сжимающих усилий. Ранее назывался «пресс Брама», так как изобретён и запатентован Джозефом Брама в 1795 году.

Гидравлический пресс состоит из двух сообщающихся цилиндров с поршнями разного диаметра (рис. 89). Цилиндр заполняется водой, маслом или другой подходящей жидкостью. По закону Паскаля давление в любом месте неподвижной жидкости одинаково по всем направлениям и одинаково передается по всему объёму. Силы, действующие на поршни, пропорциональны площадям этих поршней.

Пусть 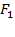и 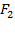–силы, действующие на поршни со стороны находящихся на них гирь. Докажем, что жидкость в цилиндрах будет находиться в равновесии лишь тогда, когда сила, действующая на большой поршень, во столько раз превышает силу, действующую на меньший поршень, во сколько раз площадь большего поршня превышает площадь меньшего поршня. Для этого заметим, что жидкость будет оставаться в равновесии только тогда, когда давления под поршнями будут одинаковыми: 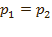.Но каждое из этих давлений можно выразить через силу и площадь: 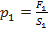; 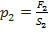. Таким образом, 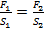,откуда 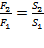,что и требовалось доказать.

Отношение 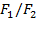характеризуетвыигрыш в силе, получаемый в данной машине. Согласно полученной формуле выигрыш в силе определяется отношением площадей 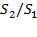. Поэтому, чем больше отношение площадей поршней, тем больше выигрыш в силе.

Гидростатическое давление

Рассмотрим равновесие однородной жидкости, находящейся в поле тяготения Земли. На каждую частицу жидкости, находящейся в поле тяготения Земли, действует сила тяжести. Жидкости и газы передают по всем направлениям не только оказываемое на них внешнее давление, но и то давление, которое существует внутри их благодаря весу собственных частей. Верхние слои жидкости давят на средние слои, те - на нижние, а последние – на дно.

Давление, оказываемое покоящейся жидкостью, называется гидростатическим.

Получим формулу для расчета гидростатического давления жидкости на произвольной глубине 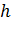в окрестности точки ( рис. 90).

Сила давления, действующая в этом месте со стороны вышележащего узкого вертикального столба жидкости, может быть выражена двумя способами: во-первых, как произведение давления в основании этого столба на площадь его сечения:

;

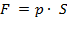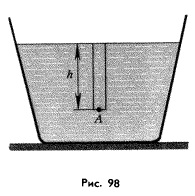Рис. 90.

во-вторых, как вес того же столба жидкости, т. е. произведение массы жидкости на ускорение свободного падения : .

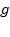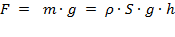Приравняем оба выражения для силы давления:

.

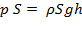Разделив обе части этого равенства на площадь , найдем давление жидкости на глубине : ,

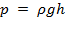где 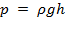– гидростатическое давление, – плотность жидкости, – высота столба жидкости.

Мы получили формулу гидростатического давления: гидростатическое давление на любой глубине внутри жидкости не зависит от формы сосуда, в котором находится жидкость, и равно произведению плотности жидкости, ускорения свободного падения и глубины, на которой рассматривается давление.

Одно и то же количество воды, находясь в разных сосудах, может оказывать разное давление на дно. Поскольку это давление зависит от высоты столба жидкости, то в узких сосудах оно будет больше, чем в широких. Благодаря этому даже небольшим количеством воды можно создать очень большое давление.

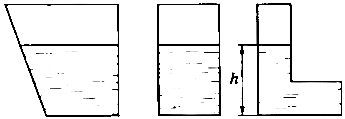Рис. 91.

Давление жидкости на дно не зависит от формы сосуда, а определяется только высотой уровня жидкости и ее плотностью. Во всех случаях, приведенных на рисунке 91, давление жидкости на дно сосудов одинаково.

Жидкость давит на данной глубине одинаково по всем направлениям – не только вниз, но и вверх, и в стороны. Следовательно, давление на стенку на данной глубине будет таким же, как и давление на горизонтальную площадку, расположенную на той же глубине.

Если над свободной поверхностью жидкости создается давление 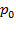то давление в жидкости на глубине будет: .

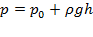Силы давления на дно и на стенки можно рассчитать по формулам:

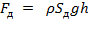– сила давления жидкости на горизонтальное дно, где 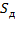– площадь дна;

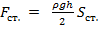– сила давления жидкости на боковую прямоугольную вертикальную стенку сосуда, где 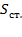– площадь стенки.

Пример.В покоящейся жидкости свободная поверхность жидкости всегда горизонтальна. Нередко встречаются случаи, когда жидкость, покоясь относительно сосуда, движется вместе с ним. Если при этом сосуд движется равномерно и прямолинейно, то свободная поверхность жидкости будет горизонтальна. Но если сосуд движется с ускорением, то ситуация меняется и возникают вопросы о форме свободной поверхности жидкости, о распределении давления в ней.

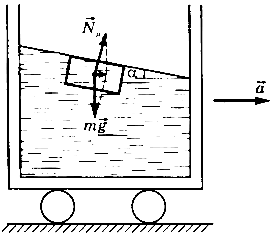Рис. 92.

Так, в случае горизонтального движения сосуда с ускорением в поле тяготения Земли любая часть жидкости массой 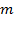движется с тем же ускорением под действием равнодействующей силы давления 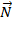, действующей со стороны остальной жидкости и силы тяжести 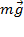(рис. 92).

Основное уравнение динамики: .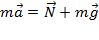

В результате свободная поверхность жидкости не будет горизонтальна, а образует с горизонтом угол , который можно легко найти, если спроецировать основное уравнение динамики на горизонтальную и вертикальную оси:

; .

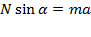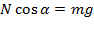Отсюда: .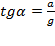

Давление на горизонтальную поверхность (горизонтальное дно) будет возрастать в направлении, противоположном ускорению.

Закон Архимеда. Условия плавания тел