Динамика вращательного движения
Из всех видов вращательного движения будем рассматривать только вращение тела вокруг неподвижной оси.
Момент силы
Момент силы, величина, характеризующая вращательный эффект силы при действии её на твёрдое тело; является одним из основных понятий механики. Различают момент силыотносительно центра (точки –полюса) и относительно оси.
Моментом силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) относительно неподвижной точки 0 (полюса) называется векторная величина 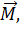 равная векторному произведению радиус – вектора
равная векторному произведению радиус – вектора 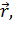 проведённого из точки 0 (полюса) в точку А приложения силы, на вектор силы
проведённого из точки 0 (полюса) в точку А приложения силы, на вектор силы 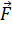 :
: 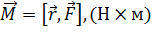 .
.
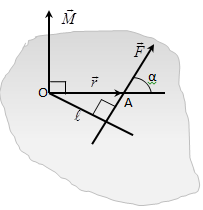 Рис. 66.
Рис. 66.
|
Направлен вектор 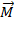 перпендикулярно плоскости, проходящей через 0 и
перпендикулярно плоскости, проходящей через 0 и 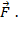 Сторона, куда направляется
Сторона, куда направляется 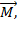 выбирается условно. При правой системе координат вектор
выбирается условно. При правой системе координат вектор 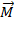 направляют в ту сторону, откуда поворот, совершаемый силой, виден против хода часовой стрелки.
направляют в ту сторону, откуда поворот, совершаемый силой, виден против хода часовой стрелки.
Момент силы– аксиальный вектор. Он направлен вдоль оси вращения. Направление вектора момента силы определяется правилом буравчика (рис.67).
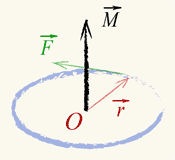 Рис. 67.
Рис. 67.
|
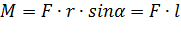 ,где:
,где: 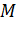 – момент силы,
– момент силы,  – приложенная сила,
– приложенная сила,  – расстояние от центра вращения до места приложения силы,
– расстояние от центра вращения до места приложения силы, 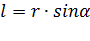 .– плечо силы, т.е. длина перпендикуляра, опущенного из центра вращения на линию действия силы,
.– плечо силы, т.е. длина перпендикуляра, опущенного из центра вращения на линию действия силы, 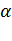 – угол, между вектором силы
– угол, между вектором силы 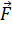 и вектором положения
и вектором положения  . Т.е. численно момент силы равен произведению модуля силы
. Т.е. численно момент силы равен произведению модуля силы  на плечо
на плечо  .
.
Направление момента силы можно также определить по правилу левой руки: четыре пальца левой руки поставить по направлению первого сомножителя  , второй сомножитель
, второй сомножитель 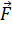 входит в ладонь, отогнутый под прямым углом большой палец укажет направления момента силы
входит в ладонь, отогнутый под прямым углом большой палец укажет направления момента силы 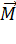 . Вектор момента силы всегда перпендикулярен плоскости, в которой лежат векторы
. Вектор момента силы всегда перпендикулярен плоскости, в которой лежат векторы  и
и 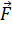 .
.
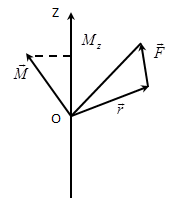 Рис. 68.
Рис. 68.
|
Моментом силы
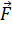 относительно неподвижной оси
относительно неподвижной оси 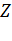 называется скалярная величина равнаяпроекции на эту ось вектора момента силы
называется скалярная величина равнаяпроекции на эту ось вектора момента силы 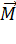 , определённого относительно произвольной точки
, определённого относительно произвольной точки 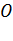 данной оси
данной оси 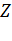 (рис. 68). Момент силы относительно оси величина алгебраическая.
(рис. 68). Момент силы относительно оси величина алгебраическая.
Пользуясь понятием момента силы можно по-новому сформулировать условия равновесия тела, закрепленного на оси. Это условие называется правилом моментов :если на тело, закрепленное на оси, действует много сил, то для равновесия тела, закрепленного на оси, алгебраическая сумма моментов всех сил, действующих на тело, должна быть равна нулю:
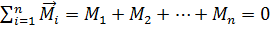 .
.
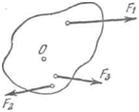 Рис. 69.
Рис. 69.
|
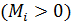 , если эта сила, действуя в отдельности, вращала бы тело по часовой стрелке, и отрицательным
, если эта сила, действуя в отдельности, вращала бы тело по часовой стрелке, и отрицательным 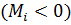 в противоположном случае (при этом нужно заранее условиться, с какой стороны мы будем смотреть на тело). Например, согласно рис.69, силам
в противоположном случае (при этом нужно заранее условиться, с какой стороны мы будем смотреть на тело). Например, согласно рис.69, силам 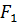 и
и 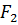 следует приписать положительный момент, а силе
следует приписать положительный момент, а силе 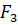 – отрицательный.
– отрицательный.
Примеры:
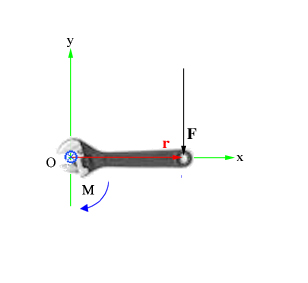 Рис. 70. Момент силы, приложенный к гаечному ключу, направлен от читателя.
Рис. 70. Момент силы, приложенный к гаечному ключу, направлен от читателя.
|
1). Гаечный ключ
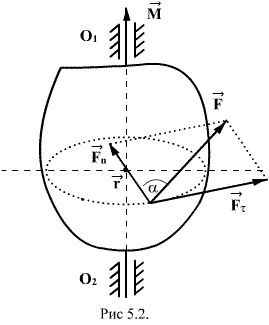 Рис. 70.
Рис. 70.
|
2). Пусть на тело, в плоскости перпендикулярной оси вращения
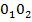 действует сила
действует сила 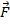 . Разложим эту силу на две составляющие:
. Разложим эту силу на две составляющие: 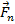 и
и 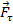 .(рис. 70).
.(рис. 70).
Сила 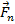 пересекает ось вращения и, следовательно, не влияет на вращение тела. Под действием составляющей
пересекает ось вращения и, следовательно, не влияет на вращение тела. Под действием составляющей 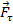 тело будет совершать вращательное движение вокруг оси
тело будет совершать вращательное движение вокруг оси 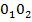 . Расстояние
. Расстояние 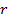 от оси вращения до линии вдоль которой действует сила
от оси вращения до линии вдоль которой действует сила 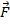 ,называется плечом силы
,называется плечом силы 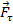 . Моментом силы относительно точки 0 называется произведение модуля силы
. Моментом силы относительно точки 0 называется произведение модуля силы 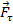 на плечо
на плечо 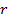 :
: 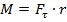 .
.
С учетом, что 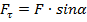 ,момент силы
,момент силы 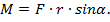 С точки зрения векторной алгебры это выражение представляет векторное произведение радиуса-вектора
С точки зрения векторной алгебры это выражение представляет векторное произведение радиуса-вектора 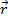 проведенного в точку приложения силы
проведенного в точку приложения силы 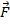 на эту силу.
на эту силу.
Таким образом, момент силы относительно точки 0 является векторной величиной и равен: 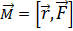 .
.
Вектор момента силы направлен перпендикулярно к плоскости, проведенной через векторы 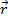 и
и 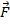 , и образует с ними правую тройку векторов (при наблюдении из вершины вектора
, и образует с ними правую тройку векторов (при наблюдении из вершины вектора 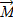 видно, что вращение по кратчайшему расстоянию от
видно, что вращение по кратчайшему расстоянию от 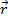 к
к 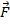 происходит против часовой стрелки).
происходит против часовой стрелки).
Примеры:
1). Рычаги
Рычагом называют имеющее неподвижную ось вращения твердое тело, на которое действуют силы, стремящиеся повернуть его вокруг этой оси.
Примерами рычагов являются гаечные ключи, различные педали, щипцы для раскалывания орехов, двери и т. д.
Согласно правилу моментов, рычаг (любого рода) уравновешен только тогда, когда 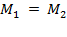 .Поскольку
.Поскольку 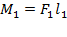 и
и 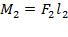 , получаем
, получаем 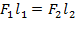 . Из последней формулы следует, что:
. Из последней формулы следует, что:
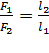 ,
,
т. е., при равновесии рычага под действием двух сил модули этих сил обратно пропорциональны их плечам. Т.е. с помощью рычага можно получить выигрыш в силе тем больший, чем больше соотношение плеч. Это широко используют на практике.
2). Пара сил
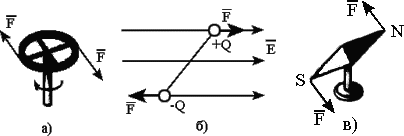 Рис. 71.
Рис. 71.
|
Две равные по модулю антипараллельные силы, приложенные к телу в разных точках, называют парой сил. Примерами пары сил могут служить силы, которые приложены к рулевому колесу автомобиля (рис.71а), электрические силы, действующие на диполь (рис.71б), магнитные силы, действующие на магнитную стрелку (рис. 71в) и т. д.
Пара сил не имеет равнодействующей, т. е. совместное действие этих сил нельзя заменить действием одной силы. Поэтому пара сил не может вызвать поступательное движение тела, а вызывает только его вращение.
Если при повороте тела под действием пары сил направления этих сил не изменяются (рис.71б, в), то поворот тела происходит до тех пор, пока обе силы не окажутся действующими противоположно друг другу вдоль прямой, проходящей через ось вращения тела.
Пусть на тело, имеющее закрепленную ось вращения О, действует пара сил  и
и  . Моменты этих сил
. Моменты этих сил 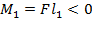 и
и 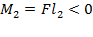 (рис. 72). Сумма моментов
(рис. 72). Сумма моментов 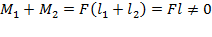 , следовательно, тело не находится в равновесии.
, следовательно, тело не находится в равновесии.
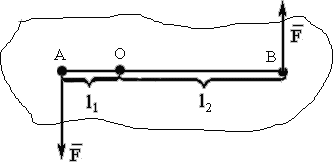 Рис. 72.
Рис. 72.
|
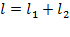 между параллельными прямыми, вдоль которых действуют силы, образующие пару сил, называют плечом пары сил:
между параллельными прямыми, вдоль которых действуют силы, образующие пару сил, называют плечом пары сил: 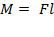 –это момент пары сил. Следовательно, момент пары сил равен произведению модуля одной из сил этой пары на плечо пары независимо от положения оси вращения тела при условии, что эта ось перпендикулярна плоскости, в которой находится пара сил.
–это момент пары сил. Следовательно, момент пары сил равен произведению модуля одной из сил этой пары на плечо пары независимо от положения оси вращения тела при условии, что эта ось перпендикулярна плоскости, в которой находится пара сил.
Если пара сил действует на тело, не имеющее закрепленную ось вращения, она вызывает вращение этого тела вокруг оси, проходящей через центр масс данного тела.
Момент импульса
Моме́нт и́мпульса (кинетический момент, угловой момент, орбитальный момент, момент количества движения) характеризует количество вращательного движения. Величина, зависящая от того, сколько массы вращается, как она распределена относительно оси вращения и с какой скоростью происходит вращение.
Следует учесть, что вращение здесь понимается в широком смысле, не только как регулярное вращение вокруг оси. Например, даже при прямолинейном движении тела мимо произвольной воображаемой точки, не лежащей на линии движения, оно также обладает моментом импульса. Наибольшую, пожалуй, роль момент импульса играет при описании собственно вращательного движения. Однако крайне важен и для гораздо более широкого класса задач (особенно – если в задаче есть центральная или осевая симметрия, но не только в этих случаях).
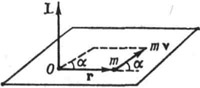 Рис. 73.
Рис. 73.
|
Момент импульса
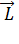 материальной точки относительно некоторого начала отсчёта (т.О – полюс) определяется векторным произведением её радиус-вектора
материальной точки относительно некоторого начала отсчёта (т.О – полюс) определяется векторным произведением её радиус-вектора  и импульса
и импульса 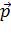 (рис. 73):
(рис. 73):
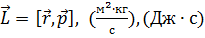 ,
,
где 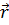 –радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта,
–радиус-вектор частицы относительно выбранного неподвижного в данной системе отсчёта начала отсчёта, 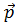 –импульс частицы.
–импульс частицы.
Модуль момента импульса равен: 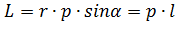 , где
, где 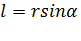 – плечо импульса, точка 0 – полюс, точка
– плечо импульса, точка 0 – полюс, точка 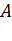 – точка приложения вектора импульса
– точка приложения вектора импульса 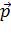 .
.
Так как момент импульса определяется векторным произведением, он является псевдовектором, перпендикулярным обоим векторам  и
и  . Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его проекцию на ось вращения как скаляр, знак которого зависит от направления вращения.
. Однако, в случаях вращения вокруг неизменной оси, бывает удобно рассматривать не момент импульса как псевдовектор, а его проекцию на ось вращения как скаляр, знак которого зависит от направления вращения.
Если выбрана такая ось, проходящая через начало отсчёта, для вычисления проекции углового момента на нее можно указать ряд приемов в соответствии с общими правилами нахождения векторного произведения двух векторов:
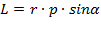 ,
,
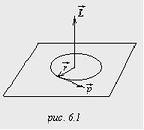 Рис. 74.
Рис. 74.
|
где
 – угол между
– угол между  и
и  , определяемый так, чтобы поворот от
, определяемый так, чтобы поворот от  к
к  производился против часовой стрелки с точки зрения наблюдателя, находящегося на положительной части оси вращения (рис. 74). Направление поворота важно при вычислении, так как определяет знак искомой проекции.
производился против часовой стрелки с точки зрения наблюдателя, находящегося на положительной части оси вращения (рис. 74). Направление поворота важно при вычислении, так как определяет знак искомой проекции.
Из определения момента импульса следует его аддитивность. Для нескольких частиц момент импульса определяется как (векторная) сумма таких членов: 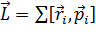 ,где
,где 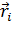 и
и 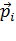 – радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется .В случае твёрдого тела задача сводится к интегрированию:
– радиус-вектор и импульс каждой частицы, входящей в систему, момент импульса которой определяется .В случае твёрдого тела задача сводится к интегрированию: 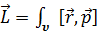 .
.
Пример:
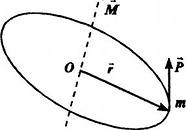 Рис. 75. На рис. момент импульса обозначен буквой
Рис. 75. На рис. момент импульса обозначен буквой 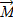 . .
|
Момент импульса материальной точки массой
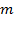 , вращающейся по окружности радиусом
, вращающейся по окружности радиусом  (рис. 75):
(рис. 75): 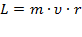 .
.
Важнейшим законом природы является закон сохранения момента импульса:в инерциальной системе отсчёта момент импульса замкнутой системы частиц остаётся постоянным: 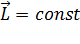 .
.
Как доказано в современной физике (теорема Э.Нетер) закон сохранения момента импульса – следствие изотропности пространства[17].
Момент инерции
Известно, что твёрдое тело при вращении приобретает определённую устойчивость (катящиеся монета, обруч).
По аналогии с первым законом Ньютона можно утверждать:
Твёрдое тело, вращающееся вокруг некоторых осей, проходящих через центр масс, не испытывает действия внешних сил и сохраняет вращение неопределённо долго.
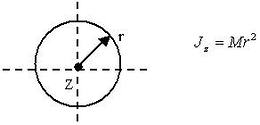 Рис. 76.
Рис. 76.
|
Пусть
 –тая материальная точка массой
–тая материальная точка массой 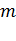 вращается по окружности радиуса
вращается по окружности радиуса  под действием силы
под действием силы 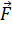 (рис. 76).
(рис. 76).
Тогда по второму закону Ньютона: 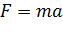 ,
, 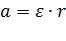 , где
, где 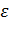 –угловое ускорение точки; отсюда следует:
–угловое ускорение точки; отсюда следует: 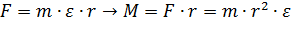 , где
, где 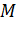 – момент силы
– момент силы  относительно оси вращения.
относительно оси вращения.
Обозначим: 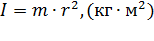 – момент инерции вращающейся точки.
– момент инерции вращающейся точки.
Тогда момент силы 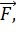 действующий на точку:
действующий на точку: 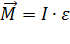 .
.
Момент инерции тела относительно оси вращения равен сумме моментов инерции всех его точек: 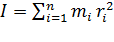 . Математически задача сводится к интегрированию.
. Математически задача сводится к интегрированию.
Момент инерцииI–скалярная величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела во вращательном движении.
Одно и то же тело может иметь различные моменты инерции относительно разных осей.
При заданном относительно тела направлении оси момент инерции тела относительно этой оси будет наименьшим, если ось проходит через центр масс тела (т. С), т.е. 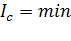 .
.
Среди осей, проходящих через центр масс тела, имеются три особые взаимно перпендикулярные оси. При равномерном вращении вокруг этих осей тело не оказывает влияния на подшипники. Эти оси называются главными осями. При произвольной форме тела нахождение их затруднительно. Но у симметричных тел положение главных осей определяется легко. Моменты инерции тела относительно главных осей называются главными моментами инерции.
Главные моменты инерции тел простой формы
| Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения | |||
| Тело | Описание | Положение оси a | Момент инерции 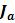
|
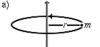
| Материальная точка массы m | На расстоянии r от точки, неподвижная | 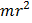
|

| Полый тонкостенный цилиндр или кольцо радиуса r и массы m | Ось цилиндра | 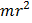
|

| Сплошной цилиндр или диск радиуса r и массы m | Ось цилиндра | 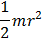
|

| Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1(труба) | Ось цилиндра | 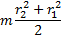
|
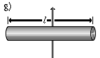
| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его центр масс | 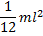
|

| Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его конец | 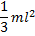
|
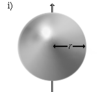
| Тонкостенная сфера радиуса r и массы m | Ось проходит через центр сферы | 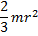
|
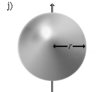
| Шар радиуса r и массы m | Ось проходит через центр шара | 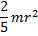
|
Теорема Штейнера
Момент инерции тела относительно произвольной оси определяется по теореме Штейнера:
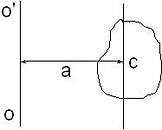 Рис. 77.
Рис. 77.
|
Момент инерции тела
 относительно произвольной оси равен сумме момента инерции
относительно произвольной оси равен сумме момента инерции 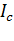 относительно оси, параллельной данной и проходящей через центр инерции тела, произведения массы тела на квадрат расстояния между осями (рис. 77).
относительно оси, параллельной данной и проходящей через центр инерции тела, произведения массы тела на квадрат расстояния между осями (рис. 77).
где 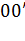 - произвольная ось,
- произвольная ось, 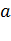 – расстояние между осями.
– расстояние между осями.
Математическая формулировка теоремы Штейнера: 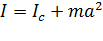 ,где
,где 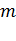 – масса тела.
– масса тела.
Пример.
Момент инерции стержня относительно оси, проходящей через его конец, равен:
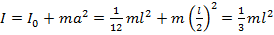 ,
,
где 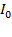 – момент инерции стержня относительно оси, проходящей через центр масс стержня.
– момент инерции стержня относительно оси, проходящей через центр масс стержня.
Уравнение динамики вращательного движения твёрдого тел относительно неподвижной оси
Из предыдущего параграфа (Момент инерции) следует, что для вращающейся по окружности  - той материальной точки справедливо соотношение:
- той материальной точки справедливо соотношение: 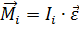 .
.
Для твёрдого тела, состоящего из 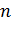 материальных точек:
материальных точек: 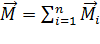 ;
; 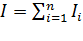 ,получаем:
,получаем: 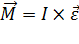 .
.
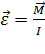 . (1)
. (1)
Уравнение (1) – уравнение динамики вращающегося твёрдого тела (основное уравнение динамики вращательного движения):
Угловое ускорение твёрдого тела, вращающегося вокруг неподвижной оси, прямо пропорционально суммарному моменту всех внешних сил, действующих на тело, и обратно пропорционально его моменту инерции.
Представим уравнение (1) в виде:
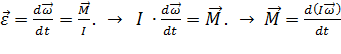 .
.
С учётом того, что 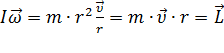 , где
, где 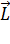 – момент импульса тела. Тогда:
– момент импульса тела. Тогда: 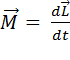 . (2)
. (2)
Уравнение (2) – так же является уравнением динамики вращающегося твёрдого тела (основное уравнение динамики вращательного движения):
Скорость изменения момента импульса тела относительно некоторой оси равна результирующему моменту относительно той же оси всех внешних сил, приложенных к телу.
Из уравнений (1) и (2) следует: 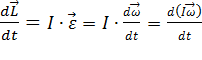 .
.
Тогда получаем: 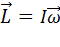 . (3)
. (3)
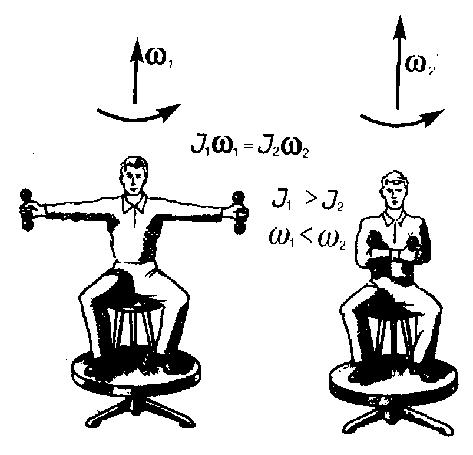 Рис. 78.
Рис. 78.
|
Если система частиц замкнута, то на неё внешние силы не действуют, то момент внешних сил
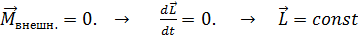 ,т.е. получен закон сохранения импульса. С учётом уравнения (3) получаем:
,т.е. получен закон сохранения импульса. С учётом уравнения (3) получаем: 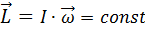 . Следовательно,
. Следовательно, 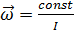 ,т.е.угловая скорость обратно пропорциональна моменту инерции тела(см. рис. 78).
,т.е.угловая скорость обратно пропорциональна моменту инерции тела(см. рис. 78).
Подобное свойство используется при исполнении фигуристами пируетов на льду, сальто акробатами.
Кинетическая энергия вращающегося твёрдого тела
Вращающееся твёрдое тело обладает энергией.
При вращении твёрдого тела относительно неподвижной оси отдельные его элементы массы 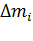 описывают окружности различных радиусов
описывают окружности различных радиусов 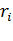 и имеют различные линейные скорости
и имеют различные линейные скорости 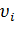 . Однако угловая скорость вращения всех точек тела одинакова:
. Однако угловая скорость вращения всех точек тела одинакова:
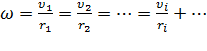 .
.
Кинетическая энергия тела – сумма кинетических энергий всех его тоек:
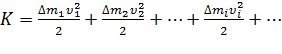 .Т.к.
.Т.к. 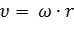 , то получаем:
, то получаем:
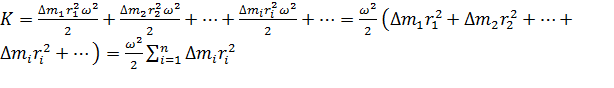 . Учтём, что момент инерции тела равен сумме моментов инерции всех его точек :
. Учтём, что момент инерции тела равен сумме моментов инерции всех его точек : 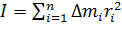 .
.
С учётом последнего соотношения получаем окончательное выражение для кинетической энергии вращающегося твёрдого тела:
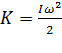 .
.
В случае плоского движения твёрдого тела его полная кинетическая энергия равна:
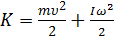 .
.
Аналогия между поступательным и вращательным движениями
Между движением твердого тела вокруг неподвижной оси и движением отдельной материальной точки (или поступательным движением тела) существует тесная и далеко идущая аналогия. Каждой линейной величине из кинематики точки соответствует подобная величина из кинематики вращения твердого тела. Координате 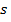 соответствует угол
соответствует угол 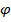 , линейной скорости
, линейной скорости 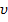 , угловая скорость
, угловая скорость 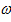 , линейному (касательному) ускорению
, линейному (касательному) ускорению 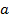 – угловое ускорение
– угловое ускорение 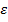 .
.
| Поступательное движение | Вращательное движение | ||||
| Кинематические характеристики движения | |||||
| Путь | S | м | Угол поворота | j | рад |
| Время | t | с | Период | Т | с |
| Скорость | 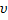
| м/с | Угловая скорость | w | рад/с |
| Ускорение | a | м/с2 | Угловое ускорение | e | рад/с2 |
| Динамические характеристики движения | |||||
| Масса | m | кг | Момент инерции | J | кг×м2 |
| Сила | F | Н | Момент силы | M | Н×м |
| Импульс | P | кг×м/с | Момент импульса | L=J×w | кг×м2 /с |
| Второй закон Ньютона | F=ma; F=dp/dt | Уравнение динамики вращательного движения | M=J×e; M=dL/dt | ||
| Работа | dA=F×dS | Дж | Работа | dA=M×dj | Дж |
| Кинетическая энергия | EK=(m 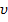 2)/2 2)/2
| Дж | Кинетическая энергия | EKВР=(Jw2)/2 | Дж |
| Мощность | N=F 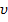
| Вт | Мощность | N=М×w | Вт |
Поступательное движение можно рассматривать, как вращательное, с радиусом вращения, стремящимся к бесконечности, и угловой скоростью, стремящейся к нулю.
 Рис. 79.
Рис. 79.
|
5. Механический (классический) принцип относительности
(принцип относительности Галилея)
Краткая биография Г.Галилея
ГАЛИЛЕЙ Галилео (15.II.1564 – 8.I.1642) – выдающийся итальянский физик и астроном, один из основателей точного естествознания, член Академии де Линчей (1611 г.), родился в Пизе. В 1581 г. поступил в Пизанский университет, где изучал медицину. Но, увлекшись геометрией и механикой, в частности сочинениями Архимеда и Евклида, оставил университет с его схоластическими лекциями и вернулся во Флоренцию, где четыре года самостоятельно изучал математику.
С 1589 г.– профессор Пизанского ун-та, в 1592 –1610 гг.– Падуанского, в дальнейшем – придворный философ герцога Козимо II Медичи.
Оказал значительное влияние на развитие научной мысли. Именно от него берет начало физика как наука. Галилею человечество обязано двумя принципами механики, сыгравшими большую роль в развитии не только механики, но и всей физики. Это известный галилеевский принцип относительности для прямолинейного и равномерного движения и принцип постоянства ускорения силы тяжести.
Галилей установил закон инерции (1609), законы свободного падения, движения тела по наклонной плоскости (1604 – 09) и тела, брошенного под углом к горизонту, открыл закон сложения движений и закон постоянства периода колебаний маятника (явление изохронизма колебаний, 1583). От Галилея ведет свое начало динамика.
В июле 1609 г. Галилей построил свою первую подзорную трубу – оптическую систему, состоящую из выпуклой и вогнутой линз, – и начал систематические астрономические наблюдения. Это было второе рождение подзорной трубы, которая после почти 20-летней неизвестности стала мощным инструментом научного познания. Поэтому Галилея можно считать изобретателем первого телескопа. Он достаточно быстро усовершенствовал свою подзорную трубу и, как писал со временем, «построил себе прибор в такой степени чудесный, что с его помощью предметы казались почти в тысячу раз больше и более чем в тридцать раз ближе, чем при наблюдении простым глазом». В трактате «Звездный вестник», вышедшем в Венеции 12 марта 1610 г., он описал открытия, сделанные с помощью телескопа: обнаружение гор на Луне, четырех спутников у Юпитера, доказательство, что Млечный Путь состоит из множества звезд.
Астрономические открытия Галилея сыграли огромную роль в развитии научного мировоззрения, они со всей очевидностью убеждали в правильности учения Коперника, ошибочности системы Аристотеля и Птолемея, способствовали победе и утверждению гелиоцентрической системы мира. В 1632 г. вышел известный «Диалог о двух главнейших системах мира», в котором Галилей отстаивал гелиоцентрическую систему Коперника. Выход книги разъярил церковников, инквизиция обвинила Галилея в ереси и, устроив процесс, заставила публично отказаться от коперниковского учения, а на «Диалог» наложила запрет. После процесса в 1633 г. Галилей был объявлен «узником святой инквизиции» и вынужден был жить сначала в Риме, а затем в Арчертри близ Флоренции. Однако научную деятельность Галилей не прекратил, до своей болезни (в 1637 г. Галилей окончательно потерял зрение) он завершил труд «Беседы и математические доказательства, касающиеся двух новых отраслей науки», который подводил итог его физических исследований.
Изобрел термоскоп, являющийся прообразом термометра, сконструировал (1586 г.) гидростатические весы для определения удельного веса твердых тел, определил удельный вес воздуха. Выдвинул идею применения маятника в часах. Физические исследования посвящены также гидростатике, прочности материалов и т. п.
Сочинения:
1. Диалог о двух главнейших системах мира Птоломеевой и Коперниковой. М.–Л. ОГИЗ, 1948.
2. Пробирных дел мастер / Пер. Ю. А. Данилова. – М.: Наука, 1987. – 272 с. – (Серия «Популярныепроизведения классиков естествознания»).
3. Беседы и математические доказательства, касающиеся двух новых отраслей наук (Сочинения. т.1). ГТТИ. М–Л. 1934.
4. Рассуждения о телах, плавающих в воде, и о тех, которые в ней движутся.В кТ: Архимед. Стэвин. Галилей. Паскаль.Начала гиростатики. Серия "Классики естествознания"» ГНТТИ. М.-Л. 1933.
Механический принцип относительности
Принцип относительности – это принцип равноправия инерциальных систем отсчёта (ИСО) в классической механике, проявляющегося в том, что законы механики во всех таких системах одинаковы, был установлен Г.Галилеем в 1636 г.
Одинаковость законов механики для инерциальных систем Галилей иллюстрировал на примере явлений, происходящих под палубой корабля, покоящегося или движущегося равномерно и прямолинейно (относительно Земли, которую можно с достаточной степенью точности считать инерциальной системой отсчёта): «Заставьте теперь корабль двигаться с любой скоростью и тогда (если только движение будет равномерным и без качки в ту и другую сторону) во всех названных явлениях вы не обнаружите ни малейшего изменения и ни по одному из них не сможете установить, движется ли корабль или стоит неподвижно... Бросая какую-нибудь вещь товарищу, вы не должны будете бросать ее с большей силой, когда он будет находиться на носу, а вы на корме, чем когда ваше взаимное положение будет обратным; капли, как и ранее, будут падать в нижний сосуд, и ни одна не упадет ближе к корме, хотя, пока капля находится в воздухе, корабль пройдет много пядей» («Диалог о двух главнейших системах мира птоломеевой и коперниковой», М. – Л., 1948, с. 147).
Движение материальной точки относительно: её положение, скорость, вид траектории зависят от того, по отношению к какой системе отсчёта (телу отсчёта) это движение рассматривается. В то же время законы классической механики, т. е. соотношения, которые связывают величины, описывающие движение материальных точек и взаимодействие между ними, одинаковы во всех инерциальных системах отсчёта. Относительность механического движения и одинаковость (безотносительность) законов механики в разных инерциальных системах отсчёта и составляют содержание принципа относительности Галилея .Сам принцип логически следует из известных преобразований Галилея.
Преобразова́ния Галиле́я – в классической механике преобразования координат и скорости при переходе от одной инерциальной системы отсчета (ИСО) к другой.
Эти преобразования справедливы лишь при скоростях много меньше скорости света в вакууме 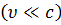 и основываются на двух предположениях, которые принимались неявно и считались очевидными:
и основываются на двух предположениях, которые принимались неявно и считались очевидными:
- ход времени одинаков во всех инерциальных системах отсчета;
- линейные размеры тела не зависят от скорости его движения относительно системы отсчета.
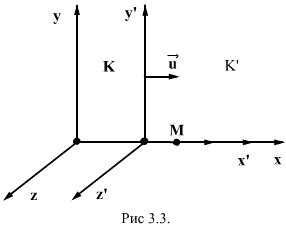 Рис. 80.
Рис. 80.
|
Пусть имеются две инерциальные системы отсчёта, одну из которых,
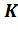 , условимся считать покоящейся; вторая система,
, условимся считать покоящейся; вторая система, 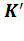 , движется по отношению к
, движется по отношению к 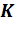 с постоянной скоростью
с постоянной скоростью 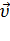 так, как показано на рис. 80.
так, как показано на рис. 80.
Тогда преобразования Галилея имеют вид:
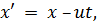
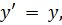
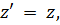
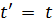
или, используя векторные обозначения,
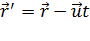 ,
,
(последняя формула остается верной для любого направления осей координат).
Из преобразований Галилея следуют:
- классический закон сложения скоростей: 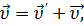 где
где 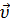 – скорость точки М в «неподвижной» системе отсчета
– скорость точки М в «неподвижной» системе отсчета 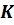 ,
, 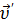 ’ – скорость точки М в движущейся системе
’ – скорость точки М в движущейся системе 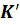 ;
;
- инвариантность (неизменность) ускорения точки М и сил, действующих на неё:
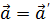 ,
,
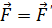 .
.
Из последних соотношений следует, что уравнение второго закона Ньютона не изменяется при переходе от одной ИСО к другой, т.е. законы Ньютона инвариантны к преобразованиям Галилея.
Современные формулировки классического принципа относительности:
1). Во всех ИСО при одних и тех же условиях все механические явления протекают одинаково.
2). Законы классической механики инвариантны относительно перехода их одной ИСО в другую.
В современной физике показано, что классический принцип относительности свидетельствует о том, что все ИСО равноправны, «абсолютной» системы отсчета нет.
Принцип относительности Галилея справедлив лишь в классической механике, в которой рассматриваются движения со скоростями, много меньшими скорости света. При скоростях, близких к скорости света, движение тел подчиняется законам релятивистской механики Эйнштейна, которые инвариантны по отношению к другим преобразованиям координат и времени Лоренца. Одним из постулатов специальной теории стал сформулированный Эйнштейном релятивистский принцип относительности: законы физики инвариантны относительно перехода из одной ИСО в другую.
Дата добавления: 2016-09-26; просмотров: 9172;











