Неинерциальные системы отсчёта
Неинерциальными системами отсчёта (НСО) называются системы отсчёта, движущиеся относительно инерциальной системы с ускорением.
Все реальные системы отсчёта неинерциальные. Законы Ньютона выполняются лишь в инерциальных системах отсчёта.
В НСО тело движется с ускорением и в тех случаях, когда на него внешние силы не действуют.
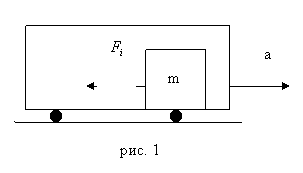 Рис. 81.
Рис. 81.
|
Например, если автобус движется с ускорением
 относительно Земли, то в системе отсчета, связанной с автобусом, на все тела будет действовать сила инерции
относительно Земли, то в системе отсчета, связанной с автобусом, на все тела будет действовать сила инерции 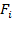 (см. рис.81).
(см. рис.81).
В НСО кроме сил, обусловленных взаимодействием, имеются силы, обусловленные неинерциальностью самих систем отсчёта, – так называемые силы инерции.
Если НСО движется с постоянным ускорением 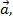 то по отношению к ней все тела, покоящиеся или движущиеся прямолинейно и равномерно по отношению к ИСО, будет двигаться с ускорением (
то по отношению к ней все тела, покоящиеся или движущиеся прямолинейно и равномерно по отношению к ИСО, будет двигаться с ускорением ( 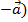 . Ускорение (
. Ускорение ( 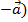 создаётся силой (
создаётся силой ( 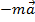 ). Эта сила и есть сила инерции.
). Эта сила и есть сила инерции.
Если тело в НСО находится во взаимодействии с другими телами, то сила инерции добавится к силам, обусловленным взаимодействием. Поэтому второй закон Ньютона в НСО имеет вид:
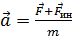 ,
,
где 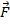 –результирующая сила, обусловленная взаимодействием тел;
–результирующая сила, обусловленная взаимодействием тел; 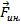 –сила инерции.
–сила инерции.
Введение сил инерции даёт возможность описывать движение тел в любых системах отсчёта с помощью одних и тех же уравнений движения, т.е. второй закон Ньютона будет справедлив в любой системе отсчёта.
В зависимости от характера движения НСО выражение для сил инерции будет иметь разный вид.
Примеры сил инерции
а) центробежная сила инерции
Центробежная сила–сила, с которой движущаяся материальная точка действует на тело (связь), стесняющее свободу движения точки и вынуждающее её двигаться криволинейно. Эта сила действует всегда только в одном направлении –от центра вращения.
Для материальной точки центробежная сила выражается формулой:
 ,
,
где:
 –центробежная сила приложенная к телу,
–центробежная сила приложенная к телу,
 –масса тела,
–масса тела,
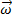 –угловая скорость вращения неинерциальной системы отсчёта относительно инерциальной (направление вектора угловой скорости определяется по правилу буравчика),
–угловая скорость вращения неинерциальной системы отсчёта относительно инерциальной (направление вектора угловой скорости определяется по правилу буравчика),
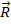 –радиус-вектор тела во вращающейся системе координат.
–радиус-вектор тела во вращающейся системе координат.
Эквивалентное выражение для центробежной силы можно записать как:
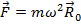 ,
,
если использовать обозначение 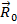 для вектора, перпендикулярного оси вращения и проведенного от неё к данной материальной точке.
для вектора, перпендикулярного оси вращения и проведенного от неё к данной материальной точке.
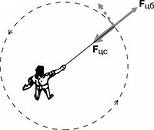 Рис. 82.
Рис. 82.
|
Центробежная сила и центростремительная сила численно равны друг другу и направлены вдоль одной прямой в противоположные стороны, но приложены к разным телам, как силы действия и противодействия. Например, при вращении в горизонтальной плоскости привязанного к верёвке груза центростремительная сила действует со стороны верёвки на груз, вынуждая его двигаться по окружности, а центробежная силадействует со стороны груза на верёвку, натягивая её (рис. 82).
б) сила Кориолиса
Си́ла Кориоли́са – одна из сил инерции, существующая в неинерциальной системе отсчёта из-за вращения и законов инерции, проявляющаяся при движении в направлении под углом к оси вращения. Названа по имени французского учёного Гюстава Гаспара Кориолиса, впервые описавшего её в статье, опубликованной в 1835 году.
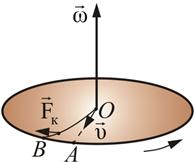 Рис. 83.
Рис. 83.
|
Появление кориолисовой силы можно обнаружить на следующем примере. Возьмем горизонтально расположенный диск, который может вращаться вокруг вертикальной оси. Прочертим на диске радиальную прямую
 (рис. 83).
(рис. 83).
Запустим в направлении от  к
к 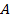 шарик со скоростью
шарик со скоростью 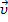 . Если диск не вращается, шарик должен катиться вдоль
. Если диск не вращается, шарик должен катиться вдоль 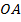 . Если же диск привести во вращение в направлении, указанном стрелкой, то шарик будет катиться по кривой
. Если же диск привести во вращение в направлении, указанном стрелкой, то шарик будет катиться по кривой 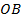 , причем его скорость относительно диска быстро изменяет свое направление. Следовательно, по отношению к вращающейся системе отсчета шарик ведет себя так, как если бы на него действовала сила
, причем его скорость относительно диска быстро изменяет свое направление. Следовательно, по отношению к вращающейся системе отсчета шарик ведет себя так, как если бы на него действовала сила 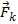 ,перпендикулярная направлению движения шарика. Действительно, при вращении диска более далёкие от центра точки движутся с большей касательной скоростью, чем менее далёкие. Переместить некоторое тело вдоль радиуса так, чтобы оно оставалось на радиусе можно, увеличив скорость тела, т. е. придав ему ускорение.
,перпендикулярная направлению движения шарика. Действительно, при вращении диска более далёкие от центра точки движутся с большей касательной скоростью, чем менее далёкие. Переместить некоторое тело вдоль радиуса так, чтобы оно оставалось на радиусе можно, увеличив скорость тела, т. е. придав ему ускорение.
Причина появления силы Кориолиса–в кориолисовом (поворотном) ускорении. В инерциальных системах отсчёта действует закон инерции, то есть, каждое тело стремится двигаться по прямой и с постоянной скоростью. Если рассмотреть движение тела, равномерное вдоль некоторого вращающегося радиуса и направленное от центра, то станет ясно, что чтобы оно осуществилось, требуется придавать телу ускорение, так как чем дальше от центра, тем должна быть больше касательная скорость вращения. Это значит, что с точки зрения вращающейся системы отсчёта, некая сила будет пытаться сместить тело с радиуса. Если вращение происходит по часовой стрелке, то двигающееся от центра вращения тело будет стремиться сойти с радиуса влево. Если вращение происходит против часовой стрелки – то вправо.
Ускорение направлено перпендикулярно векторам 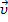 и
и 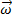 ,и максимально, если относительная скорость точки
,и максимально, если относительная скорость точки 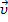 ортогональна угловой скорости
ортогональна угловой скорости 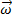 вращения подвижной системы отсчета. Кориолисово ускорение равно нулю, если угол между векторами
вращения подвижной системы отсчета. Кориолисово ускорение равно нулю, если угол между векторами 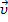 и
и 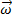 равен нулю или π, либо если хотя бы один из этих векторов равен нулю.
равен нулю или π, либо если хотя бы один из этих векторов равен нулю.
Таким образом, 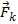 всегда лежит в плоскости, перпендикулярной к оси вращения. Сила Кориолиса возникает только в случае, когда тело изменяет свое положение по отношению к вращающейся системе отсчета.
всегда лежит в плоскости, перпендикулярной к оси вращения. Сила Кориолиса возникает только в случае, когда тело изменяет свое положение по отношению к вращающейся системе отсчета.
Пример.
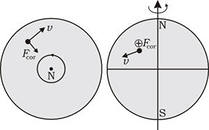 Рис. 84.
Рис. 84.
|
Пусть имеются две системы отсчёта, одна из которых
 инерциальная, а другая
инерциальная, а другая 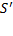 движется относительно первой произвольным образом и в общем случае является неинерциальной (рис. 84). Будем также рассматривать движение произвольной материальной точки массы
движется относительно первой произвольным образом и в общем случае является неинерциальной (рис. 84). Будем также рассматривать движение произвольной материальной точки массы 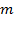 . Её ускорение по отношению к первой системе отсчёта обозначим
. Её ускорение по отношению к первой системе отсчёта обозначим 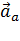 , а по отношению ко второй –
, а по отношению ко второй – 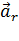 .
.
Связь между ускорениями 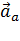 и следует из теоремы Кориолиса:
и следует из теоремы Кориолиса: 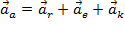 ,где
,где 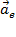 –перено́сное ускорение, а
–перено́сное ускорение, а 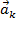 –ускорение Кориолиса (кориолисово ускорение, поворотное ускорение). Напомним, что переносным ускорением называют ускорение той точки системы
–ускорение Кориолиса (кориолисово ускорение, поворотное ускорение). Напомним, что переносным ускорением называют ускорение той точки системы  относительно системы
относительно системы  , в которой в данный момент находится рассматриваемая материальная точка.
, в которой в данный момент находится рассматриваемая материальная точка.
После умножения на массу точки и учёта второго закона Ньютона 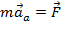 , данное соотношение можно представить в виде:
, данное соотношение можно представить в виде: 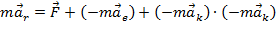 .
.
Величину 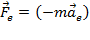 называютпереносной силой инерции, а величину
называютпереносной силой инерции, а величину 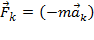 –силой Кориолиса (кориолисовой силой). Соответственно можно записать:
–силой Кориолиса (кориолисовой силой). Соответственно можно записать:
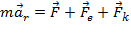 ,
,
Полученное выражение выражает основной закон динамики для неинерциальных систем отсчёта.
Из кинематики известно, что 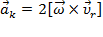 , где
, где 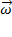 –угловая скорость вращения неинерциальной системы отсчёта
–угловая скорость вращения неинерциальной системы отсчёта 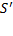 ,
, 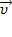 – скорость движения рассматриваемой материальной точки в этой системе отсчёта; квадратными скобками обозначена операция векторного произведения. С учётом этого для силы Кориолиса выполняется:
– скорость движения рассматриваемой материальной точки в этой системе отсчёта; квадратными скобками обозначена операция векторного произведения. С учётом этого для силы Кориолиса выполняется:
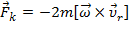 .
.
Влияние кориолисовых сил необходимо учитывать в ряде случаев при истолковании явлений, связанных с движением тел относительно земной поверхности. Например, при свободном падении тел на них действует кориолисова сила, обусловливающая отклонение к востоку от линии отвеса. Эта сила максимальна на экваторе и обращается в нуль на полюсах. Летящий снаряд также испытывает отклонения, обусловленные кориолисовыми силами инерции. Например, при выстреле из орудия, направленного на север, снаряд будет отклоняться к востоку в северном полушарии и к западу – в южном. При стрельбе вдоль экватора силы Кориолиса будут прижимать снаряд к Земле, если выстрел произведен в восточном направлении.
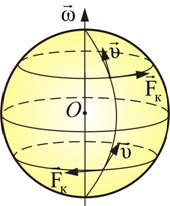 Рис. 85.
Рис. 85.
|
Сила Кориолиса действует на тело, движущееся вдоль меридиана в северном полушарии вправо и в южном – влево (рис. 85).
Это приводит к тому, что у рек подмывается всегда правый берег в северном полушарии и левый – в южном. Эти же причины объясняют неодинаковый износ рельсов железнодорожных путей.
В результате воздействия этой силы движущиеся объекты, океанские и атмосферные течения отклоняются в правую сторону в северном полушарии и в левую сторону –в южном. Это явление сильно влияет на погодные условия в масштабах всего мира. Примером действия этого эффекта является воронкообразное движение воды, выливающейся сквозь отверстие, или воздушного вихря.
Силы Кориолиса проявляются и при качаниях маятника (маятник Фуко). Для простоты предположим, что маятник расположен на полюсе. На северном полюсе сила Кориолиса будет направлена вправо по ходу маятника. В итоге траектория движения маятника будет иметь вид розетки.
В технике сила Кориолиса учитываются в теории гироскопов, турбин и многого др.
Следовательно, в общем случае, при использовании уравнений Ньютона во вращающейся системе отсчета, возникает необходимость учитывать центробежную, центростремительную силы инерции, а также кориолисову силу.
Вывод:одним из фундаментальных принципов общей теории относительности (А.Эйнштейн, 1916) является обобщённый принцип относительности:
Законы физики при одних и тех же условиях протекают одинаково в любых (инерциальных и неинерциальных) системах отсчёта.
Дата добавления: 2016-09-26; просмотров: 7473;











