Работа неконсервативных сил
Рассмотрим систему n материальных частиц.
Пусть при их взаимодействии друг с другом возникают только консервативные силы 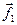 ,
, 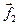 , …,
, …, 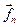 . Это внутренние силы системы. Кроме того, на элементы системы действуют и внешние силы:
. Это внутренние силы системы. Кроме того, на элементы системы действуют и внешние силы:
консервативные: 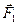 ,
, 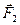 , …,
, …, 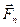
и
неконсервативные: 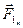 ,
, 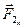 , …,
, …, 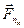 .
.
Для каждого элемента системы запишем в векторном виде уравнение движения (уравнение второго закона Ньютона):
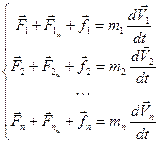 .
.
Домножим скалярно все эти уравнения на элементарные перемещения соответствующих частиц: 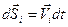 .
.
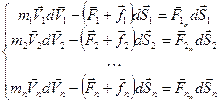 .
.
Сложим эти n уравнений:
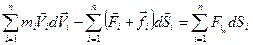 .
.
Первое слагаемое слева — изменение кинетической энергии системы:
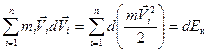 . (7.1)
. (7.1)
Второе слагаемое — это сумма работ только консервативных сил (внешних и внутренних): как мы знаем, работа консервативных сил равна изменению потенциальной энергии системы с обратным знаком, т.е. её убыли: 
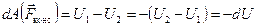 ;
;
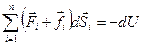 .
.
Правая часть уравнения (7.1) — это работа внешних неконсервативных сил.
Таким образом:
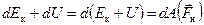 .
.
При переходе системы из состояния 1 в состояние 2:
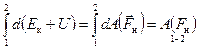 .
.
Мы пришли к следующему важному выводу:
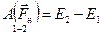 .
.
Работа, совершаемая внешними неконсервативными силами при переходе системы из одного состояния в другое, равна изменению механической энергии системы.
Следующий пример показывает, как эффектно может быть использован полученный результат при решении задач.
С наклонной плоскости высотой 0.5 м и длиной 1 м без начальной скорости соскальзывает небольшая шайба. Определить коэффициент трения шайбы о плоскость, если у основания плоскости скорость шайбы равнялась 2.45 м/с (рис. 7.2).
| h = 0.5 м l = 1 м V = 2.45 м/с |  Рис. 7.2
Рис. 7.2
|
Рассмотрим механическую энергию шайбы в начальный момент (1) и в конце спуска (2):
E1 = 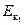 + U1 = U1 = mgh;
+ U1 = U1 = mgh;
E2 = 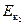 + U2 =
+ U2 = 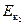 =
= 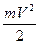 ;
;
Нулевой уровень потенциальной энергии выбран на основании наклонной плоскости.
Изменение механической энергии равно работе неконсервативных сил 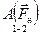 = E2 – E1. В данном случае это сила трения F = mN = mmgCosa.
= E2 – E1. В данном случае это сила трения F = mN = mmgCosa.
Работа силы трения при соскальзывании шайбы отрицательна:
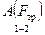 = –Fтр × l = –mmgCosa × l.
= –Fтр × l = –mmgCosa × l.
Теперь соберём все эти данные:
–mmgCosa × l = E2 – E1 = 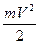 – mgh.
– mgh.
Откуда:
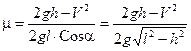 .
.
Здесь мы очень кстати вспомнили, что Cosa = 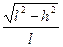 .
.
Подставив числовые значения, получим: m = 0.22.
Результат, как и следовало ожидать, безразмерный:
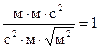 .
.
Дата добавления: 2021-01-11; просмотров: 617;











