Механическая энергия. Закон сохранения механической энергии

На прошлой лекции было введено понятие потенциальной энергии системы.

По определению разность потенциальных энергий системы в двух состояниях равна работе, совершаемой консервативными силами при переходе системы из первого состояния во второе:

.

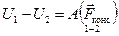Вычислим, в качестве примера, изменение потенциальной энергии пружины при её растяжении (рис. 7.1). Пусть х₁ — деформация пружины в первом состоянии, а х₂ — во втором.

Рис. 7.1

Упругая сила, согласно закону Гука, пропорциональна деформации:

F_упр = –kx.

Определим разность потенциальных энергий, подсчитав работу этой силы:

.

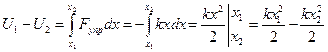Отсюда следует, что потенциальная энергия упруго деформированной пружины пропорциональна квадрату деформации:

,

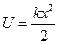а энергия недеформированной пружины (х = 0) равна нулю.

Определение разности потенциальных энергий связывает эту величину с работой консервативных сил. Если в системе действуют только консервативные силы, то работу равнодействующей этих сил при переходе системы из одного состояния в другое можно записать двояко.

Во-первых, эта работа равна разности потенциальных энергий:

.

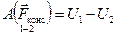С другой стороны, эта же работа равна изменению кинетической энергии системы («Теорема о кинетической энергии»):

.

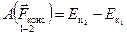Не будем упускать из виду, что речь идёт об одной и той же работе, то есть:

,

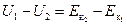или

.

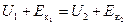Сумма кинетической и потенциальной энергий системы называется её механической энергией: Е º U + E_к.

Результат, к которому мы пришли, можно сформулировать в виде закона сохранения механической энергии: механическая энергия системы, в которой действуют только консервативные силы, остаётся постоянной:

Е = U + E_к = сonst.

Неизменность механической энергии системы ни в коем случае не означает постоянство её кинетической и потенциальной энергий. В общем случае и та и другая энергии меняются. Но при этом убыль одной энергии всегда равна росту другой. Таким образом, происходит переход потенциальной энергии в кинетическую или обратно без потери механической энергии, так, что сумма этих энергий остаётся неизменной.