Момент силы и момент импульса относительно неподвижного центра и неподвижной оси

Рассмотрим движение материальной точки m под действием силы 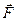. Положение этой частицы будем задавать относительно начала неподвижной системы координат радиус-вектором 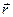(рис. 8.1).

Рис. 8.1

По определению, моментом силы 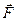относительно неподвижного центра 0 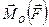называется следующее векторное произведение:

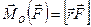. (8.1)

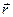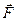Вектор момента силы перпендикулярен плоскости, образованной векторами и . Направление этого вектора связано с направлениями перемножаемых векторов «правилом правого винта».

Проекция вектора момента силы на какую-либо ось называется моментом силы относительно этой оси. Рассмотрим, например, момент силы 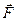относительно оси z (рис. 8.2). Разложим силу 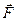на три составляющие:

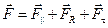
здесь: 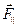— составляющая, параллельная оси z;

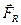— составляющая, перпендикулярная оси z и действующая вдоль прямой, проходящей через z;

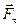— составляющая, перпендикулярная плоскости, проходящей через ось и точку приложения силы.

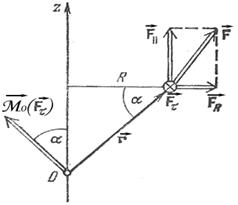
Рис. 8.2

Момент силы 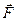относительно центра 0 можно представить теперь суммой моментов её составляющих относительного того же центра. Действительно, умножим векторно предыдущее разложение на радиус-вектор :

.

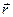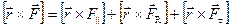В этом равенстве все слагаемые — моменты соответствующих сил:

.

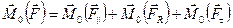Спроецируем это уравнение на ось Z

.

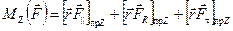Первые слагаемые равны нулю, так как векторы 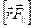и 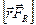перпендикулярны оси Z, поэтому их проекции на Z равны нулю.

Таким образом, момент силы 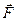относительно оси Z равен проекции на эту ось момента силы 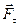относительно центра 0.

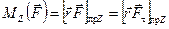
Момент силы 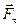относительно неподвижного центра 0:

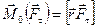
образует с осью Z угол a (см. рис. 8.2), поэтому его проекцию на эту ось следует записать так:

.

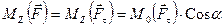Здесь 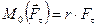, поэтому

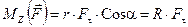. (8.2)

Здесь R=r Сosa–кратчайшее расстояние от оси вращения до точки приложения силы называется плечом силы.

Как и следовало ожидать, момент силы 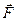относительно оси Z зависит от величины её составляющей F_t. Две другие составляющие — 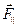и 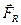— вообще не создают момента относительно оси Z.

Другой важной характеристикой вращательного движения частицы является момент импульса относительно неподвижного центра «0». Это тоже векторная величина. Она равна векторному произведению радиус-вектора частицы 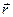на её импульс 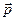= 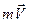(рис. 8.3).

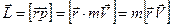. (8.3)

Модуль момента импульса равен:

L = r × mV × Sina = r × p × Sina,

где a — угол между векторам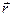и и .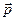

Рис. 8.3

Моментом импульса системы материальных точек называется векторная сумма их моментов импульса:

.

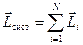Проекция вектора момента импульса на некоторую ось OZ называется моментом импульса частицы (или системы) относительно этой оси:

.

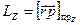Введение понятий «момент силы» и «момент импульса» обусловлено тем, что эти величины связаны друг с другом. В механике эта связь устанавливается «уравнением моментов».