Потенциальная энергия

Состояние механической системы характеризуют потенциальной энергией, если на систему действуют только консервативные силы.

Рассмотрим два состояния системы: потенциальную энергию в одном из них (в состоянии 1, например), пример условно за 0. Тогда потенциальная энергия другого состояния — 2 равна, по определению, работе, совершаемой консервативными силами при переходе системы из состояния 2 в состояние 1.

.

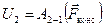Эта работа определена однозначно, так как её величина не зависит от формы траектории (рис. 6.5).

Рис. 6.5

И все же потенциальная энергия системы в состоянии 2 оказывается не однозначной, так как сохранятся произвол в выборе состояния с нулевой потенциальной энергией (1). Если считать, что нулевой энергией система обладает не в состоянии 1, а в каком-то другом состоянии — 1’, потенциальная энергия U₂ будет иной:

.

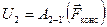Неопределенность потенциальной энергии системы становится ещё очевиднее, если учесть, что состоянию 1 (1’) мы придали нулевое значение произвольно, а можно было бы считать её равной U₁. Тогда при переходе из состояния 2 в 1 работа консервативной силы будет равна разности потенциальных энергий (рис. 6.6.)

.

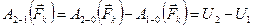Рис. 6.6

Таким образом, приходиться смириться с тем, что потенциальная энергия системы определяется не однозначно. Её величина зависит от выбора состояния с нулевой энергией.

Рассмотрим несколько примеров расчета потенциальной энергии, поясняющий её физический смысл.

Пример 1. Потенциальная энергия тела в поле тяжести Земли. Пусть тело массы т находится на высоте h над поверхностью Земли. Какова его потенциальная энергия?

Всё зависит от того, где мы выберем уровень нулевой потенциальной энергии. Пусть он будет на поверхности Земли (рис. 6.7, а), тогда

.

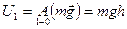Если же уровень потенциальной энергии выбрать на высоте H (H > h), то работа совершаемой силой тяжести при переходе на этот уровень будет отрицательной. Следовательно, отрицательна и потенциальная энергия тела в состоянии 1 (рис.6.7, б)

.

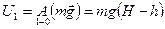Рис. 6.7

Пример 2. Вычислим энергию гравитационного притяжения двух частиц массой М и т, расположенных на расстоянии r друг от друга (рис. 6.8). Энергия такой системы считается, обычно, равной нулю, когда частицы разведены на бесконечность. Значит потенциальная энергия заданной системы равно работе, которую совершает гравитационная сила притяжения при удалении, например, массы m в бесконечность. При этом положение массы М будем считать неизменным.

Рис. 6.8

Элементарная работа гравитационной силы при удалении массы m на dr будет отрицательной:

.

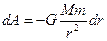Полную работу получим, вычислив интеграл:

.

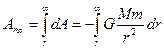Эта работа и определит искомую потенциальную энергию системы:

.

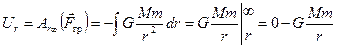Энергия оказалась отрицательной 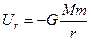. Максимальное значение энергия системы достигает при r ® ¥. Этот максимум равен нулю.