Консервативные и неконсервативные силы

Консервативными называются силы, работа которых не зависит от формы траектории, а определяется только положением её начальной и конечной точек.

К классу консервативных относятся, например, гравитационные силы, упругие, силы электростатического взаимодействия.

Вычислим, например, работу, которую совершает сила тяжести при переходах частицы разными путями из положения 1 в положение 2 (рис. 6.2). Если этот переход произошёл по вертикали, то работа силы :

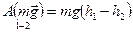. (6.11)

Теперь пусть та же частица переместится из 1 в 2 по пути 1-1’-2. Здесь промежуточная точка 1’ находится на высоте h₂.

Рис. 6.2

Полная работа будет складываться из работ силы тяжести на участках 1-1’ и 1’-2:

.

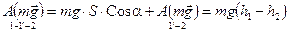Работа силы тяжести на горизонтальном участке 1’-2 равна нулю, так как здесь вектор силы нормален перемещению. Мы вновь получили прежний результат, свидетельствующий о том, что работа силы тяжести не зависит от формы траектории. Этот вывод легко обобщается и на случай произвольной криволинейной траектории, соединяющей начальную и конечную точки пути.

Гравитационная сила, сила упругости, кулоновская сила электростатического взаимодействия относятся к так называемым центральным силам.

Центральными называются силы, направленные к одной и той же точке (либо от неё). Эта точка называется силовым центром. Величина центральной силы зависит только от расстояния до силового центра r (рис. 6.3).

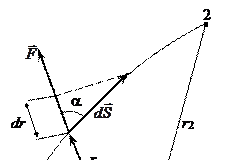Рис. 6.3

Покажем, что все центральные силы консервативны.

Вычислим работу центральной силы на участке 1-2 произвольной траектории (рис. 6.3).

Элементарная работа силы на участке :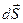

.

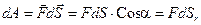Здесь dS_r = dSCosα — проекция вектора перемещения 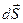на направление силы 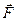(или r). Эта проекция представляет собой изменение расстояния dr до силового центра. Значит:

dA = F(r)dr.

Работа на конечном пути:

.

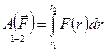Так как по определению величина центральной силы есть функция только расстояния r, то значение определённого интеграла будет зависеть только от величин r₁ и r₂, и не будет зависеть от формы траектории.

Можно дать иное определение консервативной силы.

Рассмотрим перемещение частицы из положения 1 в положение 3 под действием консервативной силы 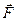(рис. 6.4).

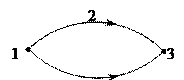
Рис. 6.4

Работа, совершаемая при этом силой 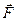, не зависит формы от траектории, то есть .

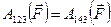Теперь вычислим работу этой же силы на замкнутом пути 1-2-3-4-1. понятно, что её можно представить суммой работ на участках 1-2-3 и 3-4-1

.

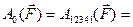
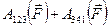При этом .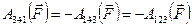

Отсюда можно заключить, что работа консервативной силы по любому замкнутому пути равна нулю

.

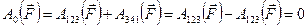Силы, работа которых на замкнутом пути не равна нулю, называются неконсервативными. К числу таких сил относятся, например, сила трения и сила вязкого сопротивления. Легко понять, что при движении частицы по замкнутому контуру работа подобных сил будет отрицательной.