Уравнение моментов для материальной точки и системы материальных точек

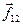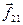Рассмотрим систему двух взаимодействующих частиц (рис. 8.4). На этом рисунке и — внутренние силы взаимодействия частиц друг с другом: = – .

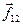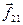Рис. 8.4

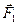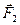и — внешние силы, действующие на частицы m₁ и m₂, 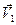и 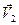— скорости частиц.

Запишем уравнения их движения (уравнения второго закона Ньютона):

+ = ;

+ = .

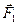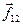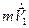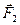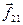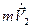Умножим векторно первое уравнение на радиус-вектор первой частицы 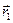, а второе — на .

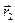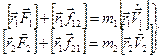. (8.3)

Заметим, что 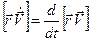. Действительно, 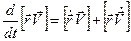. Первое слагаемое справа равно нулю, так как 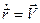. Следовательно, здесь векторно умножаются совпадающие векторы. Такое произведение равняется нулю.

Перепишем уравнения системы (8.3), учтя ещё, что :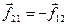

.

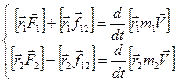Сложим эти уравнения:

.

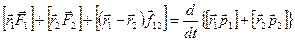Векторы 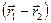и 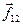коллинеарны (см. рис. 8.4), поэтому их векторное произведение равно нулю.

Окончательно это уравнение можно записать в таком виде:

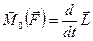. (8.4)

Здесь: 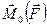— векторная сумма моментов всех внешних сил относительно центра 0;

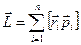— момент импульса силы относительно того же центра.

Это уравнение получило название уравнения моментов относительно неподвижного центра: производная по времени момента импульса системы материальных точек относительно произвольного неподвижного центра равна геометрической сумме моментов всех внешних сил относительно того же центра.

Уравнение моментов показывает, что изменение момента импульса системы может произойти только в результате действия момента внешних сил. Если внешние силы отсутствуют или их вращающий момент равен нулю 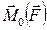= 0, то момент импульса системы остаётся неизменным во времени:

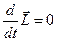, то есть 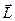= сonst.

Спроецировав уравнение (8.4) на произвольную ось Z, получим уравнение моментов относительно этой оси:

.

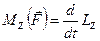Производная по времени момента импульса системы относительно оси Z равна сумме моментов внешних сил относительно этой оси.

Если сумма моментов внешних сил относительно оси равна нулю, то момент импульса системы относительно этой оси будет оставаться постоянным.