Или в матричных обозначениях

P(i + 1) = P(i)tF (2.23)

(квадратная матрица F образована из элементов P_nn¹, удовлетворяющих условиям

0 £ 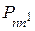£ 1 для всех n и n¹ (2.24)

и

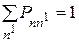для всех n). (2.25)

Всякая матрица, обладающая свойствами (2.24) и (2.25), называется стохастической; каждая ее сторона представляет стохастический вектор. Вероятности 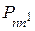называются вероятностями перехода, сама стохастическая матрица часто называется матрицей (вероятностей) перехода.

Цепь Маркова полностью определяется стохастической матрицей F и совокупностью начальных вероятностей состояний P_n(0).

Матрица перехода F может зависеть от времени, т.е. вероятности перехода 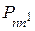могут быть функциями i, тогда

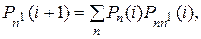
где P_n(0) и 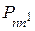(i) заданы.

Такая цепь называется неоднородной.

Наличие в матрице перехода элемента 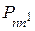, не равного нулю, указывает на то, что переход E_n ® 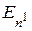возможен. Рассмотрим несколько примеров цепей Маркова.

Пример 2.3. Имеются три лотерейных круга А, В и С [2.8], каждый из которых разбит на три неравных сектора А, В и С, которые также обозначены буквами А, B и С (рис. 2.3).

Рис. 2.3. Пример, иллюстрирующий цепь Маркова

У каждого круга с параметром n (n = 1, 2, 3) центральные углы a_n, b_n и g_n, соответствующие трем секторам, измерены в таких единицах, что a_n + + b_n + g_n = 1. Производится серия испытаний, из которых начальное (нулевое) состоит в том, что случайным равновероятным образом выбирается один из кругов и этот круг приводится во вращение. Следующее испытание проводится с кругом, определенным в результате первого испытания. Назовем состоянием системы в момент i результат i-го испытания, обозначаемый одним из чисел 1, 2 или 3. Тогда получается цепь Маркова с начальными вероятностями (т.е. вероятностями в момент 0):

P₁(0) = 1/3(a₁ + a₂ + a₃),

P₂(0) = 1/3(b₁ + b₂ + b₃),

P₃(0) = 1/3(g₁ + g₂ + g₃),

где a₁ + b₁ + g₁ = 1, a₂ + b₂ + g₂ = 1, a₃ + b₃ + g₃ = 1.