Примеры решения задач. Определить вероятность p того, что время ожидания пассажиром очередного поезда не привысит 1,5 мин
Пример 2.1. Моменты прибытия вагонов метро на остановку образуют поток, приближенно являющийся потоком Пальма, причем интервал T между поездами подчинен закону равномерной плотности с характеристиками mt = 2 мин, st = 0,05 мин. Определить вероятность p того, что время ожидания пассажиром очередного поезда не привысит 1,5 мин, если пассажир приходит на станцию, не зная расписания движения поездов.
Решение
Плотность распределения времени ожидания q определяется следующей формулой:
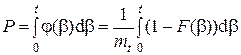 ,
,
где F(b) – функция распределения случайной величины Т, которая имеет вид
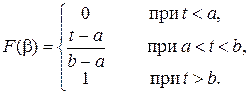
Величины a и b находим из условия
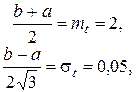
откуда а = 1,91; b = 2,09.
Следовательно,
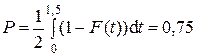 .
.
Пример 2.2. Производится воздушная разведка подвижной цели. Установлено, что время пребывания цели на одном месте подчинено следующему показательному закону:
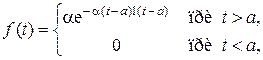
где величины а и a положительны, а 1(х) – известная единичная функция.
Кривая распределения имеет вид, показанный на рис. 2.1. Удар по разведанной цели может быть произведен лишь по истечении времени t1 после обнаружения цели разведчиком. Определить вероятность того, что к моменту нанесения удара t1 цель останется на месте ее обнаружения разведчиком, если противник не имеет сведений о действиях разведчика.

Рис. 2.1. Функция распределения к примеру 2.2
Решение
Условия задачи не изменятся, если считать, что цель на каждом месте находится случайное время Т, имеющее плотность распределения f(t). Таким образом, можно рассматривать некоторый стационарный поток Пальма с интервалом Т между соседними событиями, который условно можно назвать потоком уходов цели с места ее обнаружения.
Обнаружение цели можно рассматривать как падение случайной точки S на некоторый интервал этого потока. Следовательно, время пребывания цели на месте ее обнаружения n будет иметь плотность распределения
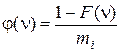 ,
,
где 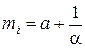 .
.
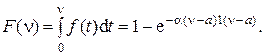
Дата добавления: 2021-01-11; просмотров: 695;











