Искомую вероятность найдем из условия

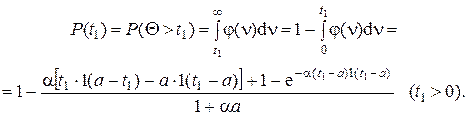
График этой функции представлен на рис. 2.2.

Рис. 2.2. График искомой вероятности

Цепи Маркова

Рассмотрим систему, которая может находиться в состояниях E_n (n = = 0, 1, 2, 3, …), причем изменения этих состояний могут происходить только в определенные моменты 0, 1, 2, …, i. Пусть P_n(i) обозначает вероятность состояния E_n в момент i. Совокупность вероятностей P_n(i), соответствующая некоторому моменту i, может быть представлена вектором в пространстве с числом измерений, равным числу возможных состояний системы (конечному или бесконечному). Этот вектор ограничен по величине и направлению условием, что все его компоненты не отрицательны и в сумме равны 1:

P(i) = (P₀(i), P₁(i), P₂(i), …), (2.19)

0 £ P_n(i) £ 1, n = 0, 1, 2, … (2.20)

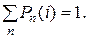(2.21)

Вектор, обладающий свойствами (2.20) и (2.21), называется стохастическим. Если его компоненты представляют вероятности состояний системы, то вектор называется вектором состояний системы.

Предположим, что переход из одного состояния в другое зависит только от этих двух состояний. Более строго, предположим, что каждой паре (E_n, 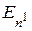) можно поставить в соответствие условную вероятность 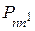того, что система находится в состоянии n¹ в момент i + 1 при условии, что она находилась в состоянии n в момент i. Считая, что начальные вероятности P_n(0) известны, получим цепь Маркова, вектор состояний которой удовлетворяет уравнениям

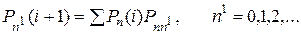, (2.22)