Нестационарный и неординарный пуассоновские потоки
Нестационарный пуассоновский поток (который также называется потоком с переменными параметрами или нестационарным простейшим потоком) есть ординарный поток без последействия, для которого в любой момент времени t существует конечный параметр l(t), зависящий от момента t. По аналогии с простейшим потоком в качестве математической модели нестационарного пуассоновского потока выбирается вероятность Рk(t0, t) поступления точно k вызовов за данный промежуток времени [t0, t). В силу нестационарности потока эта вероятность зависит не только от длины промежутка времени [t0, t), но и от начального момента t0.
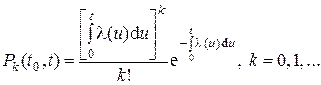 (2.14)
(2.14)
Заметим, что для стационарного потока l(n)=l, 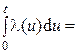
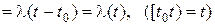 (и формула (2.14) преобразуется в (2.7)).
(и формула (2.14) преобразуется в (2.7)).
Для неординарного потока, т.е. для стационарного неординарного потока без последействия, следует различать поток вызывающих моментов и поток заявок. Поток вызывающих моментов характеризуется вероятностью появления точно i вызывающих моментов в промежутке времени t. Эта вероятность Pi(t) определяется формулой Пуассона (2.7).
В каждый вызывающий момент поступает l (1 £ l £ r) заявок. Величина l называется характеристикой неординарного потока, может быть постоянной и переменной. Если l = const, то с вероятностью Pi(t) суммарное число заявок, поступающих за отрезок времени t, составляет k = li.
Для неординарного пуассоновского потока с переменной величиной l, в котором в каждый вызывающий момент с вероятностью wi поступает l заявок ( 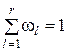 ), также получена формула, определяющая вероятность Pk(t) поступления точно k заявок за промежуток времени t (см. работу [6]). Параметр такого потока для каждого значения l равен lwi. Отсюда общий параметр для потока (
), также получена формула, определяющая вероятность Pk(t) поступления точно k заявок за промежуток времени t (см. работу [6]). Параметр такого потока для каждого значения l равен lwi. Отсюда общий параметр для потока ( 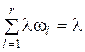 ) такой же, как и для потока вызывающих моментов, т.е. для простейшего потока. Интенсивность m неординарного пуассоновского потока, как и любого стационарного неординарного потока, больше его параметра l. Действительно,
) такой же, как и для потока вызывающих моментов, т.е. для простейшего потока. Интенсивность m неординарного пуассоновского потока, как и любого стационарного неординарного потока, больше его параметра l. Действительно,
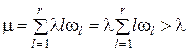 .
.
Дата добавления: 2021-01-11; просмотров: 839;











