Просеивание потоков. Потоки Эрланга

Пусть имеется поток заявок, для которого t₁, t₂, … есть моменты поступления заявок. Выберем из этого потока часть заявок, применив следующую операцию: заявка, поступающая в момент t_k (k = 1, 2, …), с вероятностью r остается в новом потоке и с вероятностью (1– r) теряется. Новый поток заявок называется просеянным. Таким образом, просеянный поток образуется из заданного потока, в котором случайное число заявок теряется, следующая заявка остается (просеивается), затем снова случайное число заявок, имеющих тот же закон распределения, теряется, следующая заявка заданного потока остается и т.д. Операция, с помощью которой получен просеянный поток, называется рекуррентной операцией просеивания. Поток, полученный из рекуррентного потока с помощью рекуррентной операции просеивания, также является рекуррентным.

Если основной поток – простейший с параметром l и каждая заявка этого потока просеивается с вероятностью r и теряется с вероятностью (1 – r), то просеянный поток будет также простейшим с параметром lr. Из этого следует весьма важный для практики вывод: если поступающий на систему обслуживания простейший поток с параметром l разделяется на h направлений и вероятность того, что вызов входящего потока поступает на i – е (i = 1, 2, …, h) направление, равна r_i, то поток i-го направления является также простейшим с параметром lr_i.

Используем отличную от рекуррентной операцию просеивания, при которой точно m заявок потока теряются, (m + 1)-я заявка просеивается, затем снова точно m заявок теряются, (m + 1)-я заявка просеивается и т.д. В результате такой операции просеивании простейшего потока образуется так называемый поток Эрланга m-го порядка. Если в простейшем потоке сохранить (просеять) каждую третью заявку, то образуется поток Эрланга 2-го порядка, каждую вторую заявку – поток Эрланга 1-го порядка. Естественно, простейший поток можно рассматривать как поток Эрланга нулевого порядка.

В потоках Эрланга любого порядка промежутки времени между заявками независимы и распределены по одному и тому же закону, так как эти промежутки представляют сумму одинакового числа промежутков простейшего потока. В связи с этим потоки Эрланга являются рекуррентными.

Математическое ожидание M(z_m), дисперсия D(z_m) и среднее квадратическое отклонение s(z_m) промежутка времени между заявками в потоке Эрланга m-го порядка можно записать следующим образом:

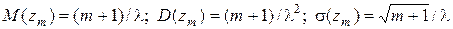, (2.17)