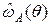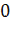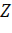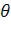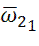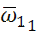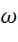Основы теории стохастической индикации

Индикатор любого случайного события 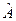является случайной величиной, обладающей следующими свойствами [7,11]

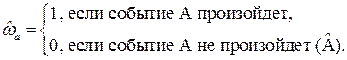(7.1)

Из соотношения (7.1) следует

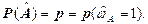(7.2)

Поскольку случайные переменные обозначаются символом 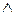, то сформулированный выше (2.2) единожды неопределённый предикат 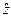< 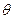будет представлять собой неопределённое высказывание или, другими словами, случайное событие 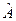. Здесь неопределённость ситуации заложена в неопределённость переменной 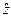, являющейся случайной величиной. Для определения вероятности p этого высказывания достаточно знать закон распределения (функцию распределения) случайной величины (нагрузки) 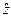и заданное значение сопротивляемости (прочности) 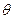, то есть

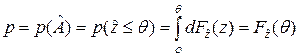. (7.3)

Пусть 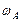- индикатор множества A = ( 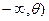. Тогда из выражений (7.2),(7.3) следует, что

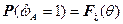, (7.4)

а плотность 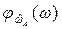и функция распределения 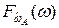случайной величины 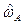примут вид [7,11,12]

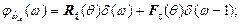(7.5)

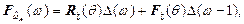(7.6)

где 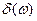- дельта-функция;

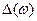- единичная функция.

Поскольку противоположные гипотезы A и 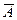всегда образуют полную группу, поэтому всегда имеет место формула

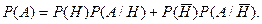
На основе (7.5), (7.6) числовые характеристики индикатора 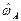могут быть определены следующим образом [5]

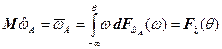; (7.7)

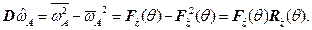(7.8)

Таким образом, как это следует из выражения (7.7), вероятность случайного события 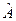равна математическому ожиданию его индикатора 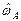[5].

В рассматриваемом случае (7.8) дисперсия 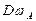характеризует степень неопределённости предиката

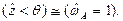
При этом, как это следует из свойств плотности 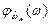, максимальная неопределённость будет при медианном значении случайной величины , то есть 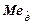[5,7].

Пусть в предикате 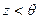, случайной является переменная 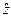. Тогда будет иметь место единожды неопределённый предикат 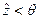, то есть случайное событие 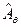, зависящее от неслучайной переменной 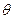. Тогда

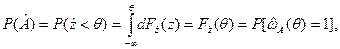(7.9)

где 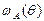- индикатор множества A = .

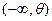Из выражения (7.9) видно, что в рассматриваемом случае

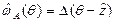. (7.10)

Индикатор 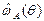графически представлен на рис 7.1

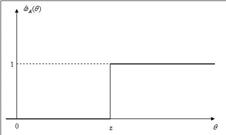
Рис 7.1 Индикатор 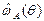случайного события .

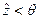Пусть переменная 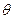также случайна, тогда имеет место неравенство 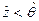и, следовательно, случайное событие 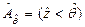, в свою очередь, зависит также и от случайной величины 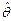. В этом случае предикат 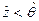становится уже дважды неопределённым.

При этом сразу же встаёт задача определения вероятности события .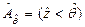

При независимости случайных величин 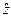и 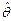, что является наиболее важной практической задачей с учетом (7.9) и формулы полной вероятности, а также с учетом возможных значений случайных величин 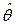и 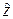, имеют место зависимост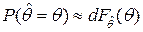и и 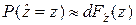, откуда

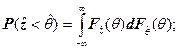(7.11)

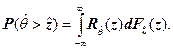(7.12)

С учётом изложенного выше ввёдем в выражениях (7.11), (7.12) следующие обозначения

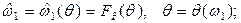(7.13)

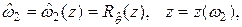(7.14)

с учётом которых выражения (7.11) и (7.12) преобразуются к виду

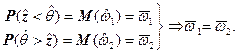(7.15)

Случайные величины 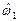и 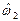называются стохастическими индикаторами.

Из (7.11), (7.12), (7.13) следует, что

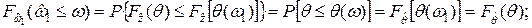
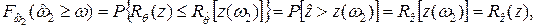
откуда 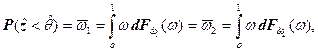(7.16)

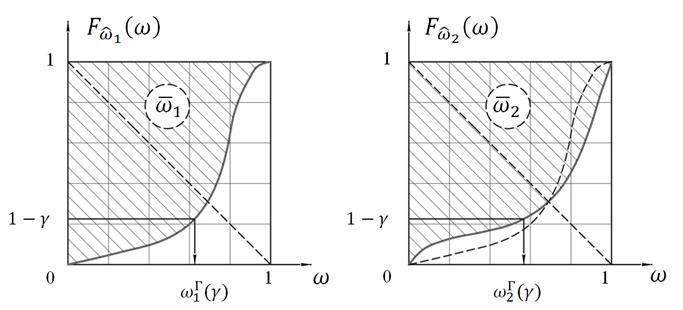
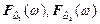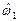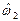где - соответственно функции распределения индикаторов и , представленные в единичных квадратах на рис. 7.2а, 7.2б, на которых априорные вероятности событи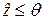й и 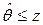равны их усредненным априорным вероятностям 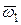и .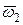

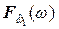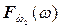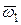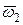Заштрихованные площади над кривыми функций распределения и , показанные на рис. 7.2а и 7.2б, геометрически представляют собой математические ожидания и случайных величин 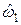и .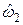

Кроме того, обозначив через 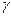уровень гарантии интересующего нас события, то есть вероятность того, что событие 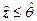или 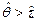произойдет (станет достоверным), можно, отложив на оси ординат значение 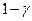, и, войдя с ним в графики (рис. 7.2а и 7.2б) до пересечения с кривыми 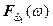, , 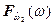и, отложив на оси абсцисс точку пересечения, получить значения 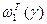и 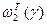, то есть гарантированные значения вероятностей выполнения событи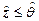й или .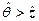

Рисунок 7.2б – Функция распределения 2-го стохастического индикатора.

Рисунок 7.2a – Функция

распределения

1-го стохастического

индикатора.