Физическая природа стохастических индикаторов.

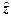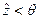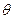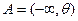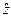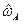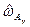Физический смысл этих свойств стохастических индикаторов заключается в следующем. Если переменная случайна, то в предикате константа определяет границу детерминированного множества , при попадании в которое случайной величины индикаторы и принимают значение 1. В этом случае достоверность событи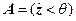й и 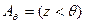равна 1.

В дважды неопределенном предикате 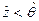переменная 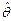определяет границу “неопределённого” (“случайного”) множества 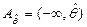, при попадании в которое случайной величины 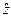индикаторы могут принимать уже любые значения на интервале (0,1]. Это объясняется тем, что в данном случае как размеры, так и расположение множества 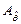и вероятность попадания случайной величины 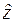в такое множество будет также случайной.

При этом вероятность 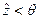представляет собой функцию распределения случайной величины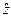

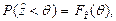
а вероятность предиката 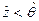будет уже представлять собой функцию случайного аргумента – случайный индикатор 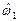, поэтому

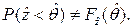(7.17)

Причём левая часть выражения (7.17) представляет собой число – математическое ожидание индикатора 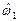, а правая часть – случайную величину – функцию случайного аргумента 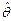- индикатор 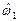[7,12].

Кроме того, понятие стохастического индикатора может быть получено непосредственно из вероятности 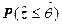, которая, в действительности, является случайной величиной, поскольку она зависит только от случайных величин 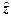и 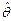. Следовательно, она является случайным индикатором 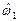этого события

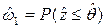. (7.18)

То же самое можно сказать и о вероятности 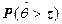, следовательно,

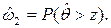
При известных функциях распределения 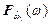и 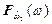случайных величин 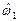и 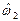математические ожидания 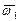и 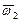с учетом (7.16) определяются следующим образом

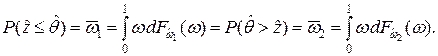(7.19)

Таким образом, математические ожидания 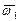и 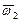стохастических индикаторов совпадают со значениями вероятностей (7.11) и (7.12), полученных на основе классических методов. Это означает, что классические методы позволяют определить только одну числовую характеристику вероятностей (7.11), (7.12). В то время как методы теории стохастической индикации являются более информативными и позволяют получить функции распределения случайных величин 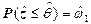и 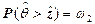, которые полностью характеризуют указанные случайные величины и позволяют получить гарантированные значения вероятносте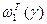й и .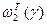

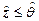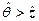При этом переменные, находящиеся в левых частях предикатов и являются управляющими переменными, а соответствующие им переменные в правых частях называются управляемыми переменными.

Например, при испытаниях и эксплуатации управляющей (трансформирующей) переменной является нагрузка 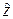, а сопротивляемость 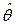является управляемой (трансформируемой) переменной. С другой стороны, на этапе проектирования сопротивляемость 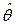является управляющей (трансформирующей) переменной, а 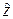– управляемой переменной. Так, в предикатах (2.45) и (2.46), левая часть является управляющей, а правая – управляемой.