Методы определения показателей надежности на основе методов стохастической индикации.

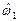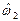Всё оказанное выше позволяет подойти к методам определения функций распределения индикаторов и при условии независимости случайных величин 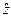и 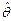. Для решения этой задачи сформулированы теоремы о функциях распределения стохастических индикаторов [11,12].

Теорема Т1. Если функции распределения 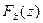и 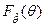независимых случайных величин 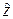и 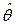известны, то

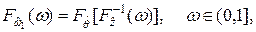( 7.20)

Доказательство. C учетом (7.13) введём обозначения:

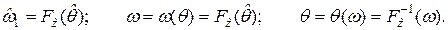
Тогда, поскольку функция 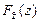неубывающая, то

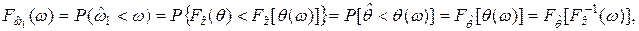
что и требовалось доказать.

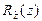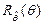Теорема Т2. Если дополнительные функции распределения и случайных величин 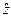и 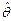известны, то

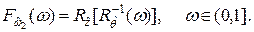(7.21)

Доказательство. C учетом (7.14) введём обозначения:

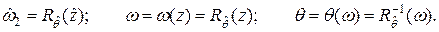
Тогда, поскольку функция невозрастающая[1], то

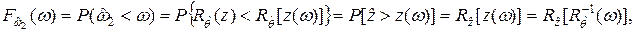что и требовалось доказать.

Пример 1. Пусть случайные величины 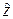и 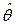обе подчинены показательным законам распределения с параметрам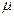и и 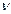соответственно:

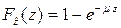, (7.22)

.

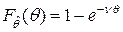Тогда согласно Т1 ( 7.20) имеем

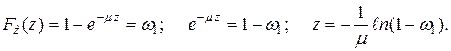(7.23)

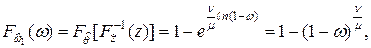(7.24)

откуда

, (7.25)

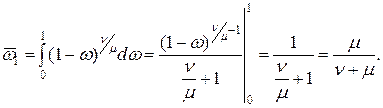(7.26)

Из (7.24) может быть получено гарантированное значение 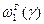вероятности безотказной работы объекта, откуда следует

,

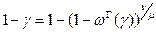откуда следует

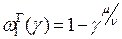. (7.27)

Формула (7.26) представляет собой математическое ожидание вероятности безотказной работы объекта. Тогда математическое ожидание вероятности отказа объекта составит

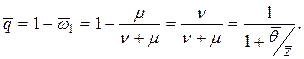(7.28)

Полученное на основе методов теории стохастической индикации выражение (7.28) для вероятности безотказной работы совпадает с её выражением (см. таблицу 3.1), полученным известными методами [2-5,16,18].

Пример 2. Пусть случайные величины 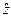и 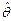распределены нормально и имеют соответственно числовые характеристик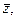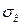и и 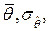то есть

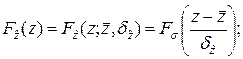(7.29)

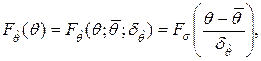(7.30)

где 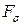(.) – нормированная по 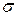функция нормального распределения (табличная функция) [2,5,18,19,22].

Тогда согласно теореме Т1 (7.20) и соотношениям (7.29), (7.30)

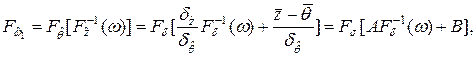(7.31)

где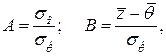

откуда

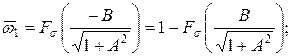(7.32)

. (7.33)

Однако в большинстве случаев вычисление показателей 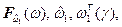а также соответственно показателей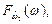 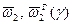в аналитической форме затруднительно и не всегда возможно. В этом случае для вычисления данных показателей предлагается графоаналитический метод, представленный на рис.7.3.

7.4 Графический метод построения функций распределения , 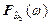стохастических индикаторов.

Исходными данными для построения являются функции распределения случайных величин 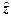и 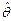, которым в зависимости от решаемой задачи может быть придана самая разнообразная смысловая нагрузка. Методика построения функций распределения и 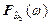представлена на рис. 7.3 (а, б, в, г).

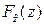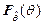Так, на рис. 7.3а приведены полученные по результатам эксплуатации и различных испытаний исходные функции распределения и случайных величин 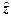и 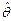. Поскольку отыскиваемые функции , 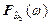полностью размещены в единичном квадрате, то такой квадрат построен справа от рис. 7.3б, ось абсцисс, которого является продолжением оси абсцисс графика, изображенного на рис. 7.3а. Далее в построенном единичном квадрате из точки на оси ординат, равной 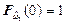, к точке 1 на оси абсцисс на графике 7.3б проводится диагональ и параллельно ей проводится ряд линий, образующих сетку с шагом 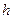, определяющим точность построения графиков и 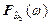. Затем из точки пересечения, например, 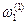любой из этих линий с осью абсцисс на рис. 7.3б необходимо двигаться по этой линии до пересечения с осью ординат, а из полученной точки пересечения необходимо двигаться параллельно осям абсцисс до пересечения с кривой 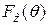(функцией распределения деформирующего распределения) на рис. 7.3а. Из полученной точки пересечения перпендикулярно оси абсцисс в направлении последней проводится линия до пересечения с кривой 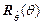(см. рис. 7.3а), а из полученной таким образом точки пересечения проводится прямая, параллельная оси абсцисс до пересечения ее с перпендикуляром, восстановленным из исходной точки 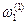. Полученная таким образом точка пересечения [ 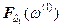] принадлежит кривой и на рис. 7.3б выделена точкой. Геометрически путь определения точек функций распределения , 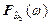на рис. 7.3а, б, в, г показан стрелками.

Затем выбирается следующая точка 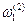из числа точек , образованных пересечением линий сетки с осью абсцисс на рис. 7.3б, и весь, описанный выше, цикл нахождения следующей точки кривой , вновь повторяется. Полученные подобным образом точки 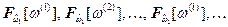соединяются плавной линией, образуя графическое представление функции распределения первого стохастического индикатора .

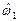Аналогичным образом на базе рис. 7.3в и 7.3г, основываясь на известных функциях 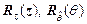, проводится графическое построение функции распределения 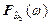второго стохастического индикатора.

б)

а)

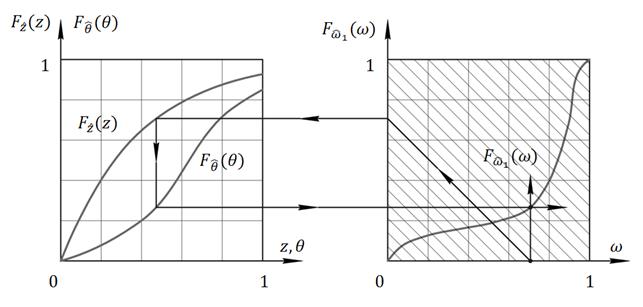
Рис. 7.3 Графическое построение функции .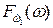

а)

б)

Рис. 7.4 Графическое построение функци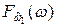и и .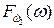

Известно, что частотная трактовка вероятности событий, в том числе рассмотренных в примере 3.1 при малом числе опытов уже не могут служить объективными характеристиками и показателями степени соответствия класса испытываемых объектов (из которого черпаются испытываемые), предъявляемым к ним требованиям [11,12]. В этих условиях получение гарантированных оценок (7.27) и (7.33) позволяют получать гарантированные оценки показателей надежности уже на этапе проектирования.

7.5. Построение функций распределения 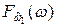и 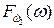стохастических индикаторов.

Данный метод наиболее предпочтителен, когда функции распределения нагрузки и сопротивляемост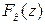и изаданы таблично или графически. Его алгоритм заключается в следующем:

1. Задают массив значени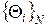й и 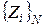, где N – объем массива

2. Случайным образом из массива 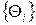выбирается одно значение 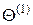, которое последовательно сравнивается со всеми значениями Z из массива .

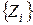3. Подсчитывается число n⁽¹⁾, непривышений нагрузкой прочности по всему числу N сравнений и на их основе вычисляется единичная оценка первого стохастического индикатора .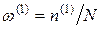

4. Затем из массива 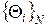по аналогии с пп. 2 и 3 вновь выбирается очередное значение 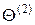, которая последовательно сравнивается со всеми значениями Z измассива 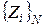и подсчитывается число n⁽²⁾ непривышений, а затем вычисляется оценка стохастического индикатора .

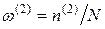5. Далее в соответствии с пп. 1-4, весь, описанный цикл вычислений, повторяется N раз, в результате чего получается массив оценок 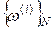, где i=1,2,3, …,N.

6. Полученные оценки 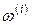располагают в порядке возрастания и получают вариационный ряд вида

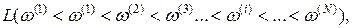(7.34)

где L – оператор, располагающий значения оценок 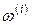в порядке их возрастания и образующий вариационный ряд значений .

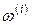7. На основе полученного вариационного ряда строится график (гистограмма) статистической функции распределения 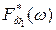первого стохастического индикатора.

Статистическая функция распределения 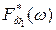второго стохастического индикатора определяется аналогичным образом.