Формулы Грина и теорема о единственности

Если произвольный вектор D не испытывает скачков в пределах некоторого объема V, то его можно представить в виде: D=y×grad(j)=y×Ñj, где y и j - некие скаляры, также непрерывные в объеме V. Для дивергенции вектора D, используя формулы дифференцирования, можно записать:

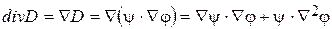
Применяя к вектору D теорему Остроградского – Гаусса заметим, что элементарный поток вектора D через любой малый элемент поверхности S, ограничивающий выбранный объем V, равен:

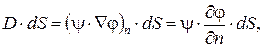
где (Ñj)_n – проекция градиента скаляра j на направление нормали к элементу поверхности dS. Подставим два полученных выражения в (1.35):

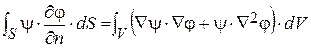. (1.36)

Выражение (1.36) называется теоремой Грина. Положим в (1.36) y = j. В областях поля, где отсутствуют заряды и удовлетворяется уравнение Лапласа: divD = Ѳj = Dj = 0, выражение (1.36) приобретает вид:

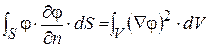. (1.37)

Выражение (1.37) известно как первая формула Грина.

Запишем выражение, аналогичное (1.36), но поменяем местами j и y.

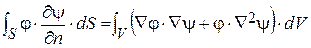(1.38)

Вычитая (1.38) из (1.36), получим выражение:

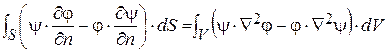, (1.39)

которое называют второй формулой Грина. Эти формулы важны при расчетах электростатических полей.

Следствие I. Из второй формулы Грина может быть получена теорема о единственности: «Решение уравнения Лапласа, удовлетворяющее заданным граничным условиям является единственным». Из теоремы о единственности следует, что для получения решения уравнения Лапласа можно применять любые способы, какими бы они ни казались на первый взгляд странными, лишь бы полученное решение удовлетворяло граничным условиям. Это решение и будет правильным и единственным верным. Доказательство теоремы проводится методом «от противного». Предположим, что существуют две различные функции, удовлетворяющие заданным граничным условиям и являющиеся решениями уравнения Лапласа: Dj º Ѳj = 0 и Dy º Ѳy = 0. Тогда правая часть второй формулы Грина (1.39) обращается в нуль при любой форме и размере объема поля V, а следовательно при любой форме ограничивающей поверхности S. Тогда подынтегральное выражение в левой части должно равняться нулю, что возможно только при условии y º j, т.е. теорема доказана.

Следствие II. Вторым важным следствием из формул Грина и теоремы о единственности является возможность замены эквипотенциальной поверхности бесконечно тонким проводящим листом. Поскольку мы рассматриваем электростатические поля, то на проводящей поверхности не может быть движущихся зарядов, т.е. не может быть разности потенциалов. В свою очередь это означает, что равна нулю составляющая напряженности поля вдоль поверхности (тангенциальная составляющая), т.е. силовые линии нормальны (перпендикулярны) проводящей поверхности. Получается, что замена любой эквипотенциальной поверхности тонким металлическим листом не нарушает картины электростатического поля и не влияет на величину потенциала и напряженности в любой точке поля. Развитием этой идеи служит замена массивного электрода со сложным распределением поверхностной плотности зарядов на тонкую проводящую поверхность, совпадающую с границей электрода. Если эта тонкая поверхность совпадает с эквипотенциальной поверхностью какого-то распределения точечных зарядов (одного или нескольких) внутри этой поверхности, то при расчетах можно заменить поле, создаваемое массивным электродом, на поле, создаваемое этими несколькими фиктивными точечными зарядами, что существенно упрощает расчеты.

Следствие III. Из первой формулы Грина (1.37) следует, что характер поля полностью определяется значениями потенциала и его производной (по нормали) на граничной поверхности. Из этого вытекает метод расчета электростатических полей, называемый «метод изображений». Суть этого метода состоит в том, что если производится расчет характеристик поля с какой-либо одной стороны эквипотенциальной поверхности, то совершенно неважно, как реально выглядит поле с другой стороны этой поверхности. На этой другой стороне поверхности (например, под землей или внутри металла) можно проводить различные замены: проводник допускается заменять на диэлектрик или наоборот, диэлектрик на другой диэлектрик и т.п., лишь бы не изменить значение потенциала и его производных на граничной поверхности.