Электрическое поле на границе раздела двух диэлектриков

На границе раздела двух диэлектриков с различными величинами диэлектрической проницаемости e₁ и e₂ выполняются следующие граничные условия:

1. тангенциальные (касательные к поверхности раздела) компоненты вектора напряженности равны между собой Е_1t = E_2t ;

2. нормальные (перпендикулярные к поверхности раздела) компоненты вектора электрического смещения равны между собой D_1n = D_2n.

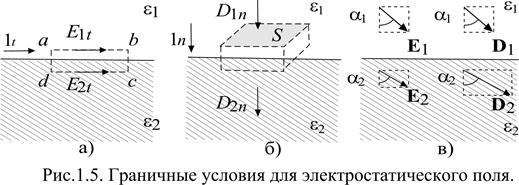
Докажем первое утверждение. Поскольку рассматриваемое поле является электростатическим, то циркуляция вектора Е равна нулю (см.§1.5). Это значит, что интеграл 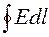по замкнутому контуру abcd (рис.1.5a) будет равен нулю. На участках ad и bc вектора E и dl выбраны взаимно перпендикулярными при построении контура abcd, т.е. их скалярное произведение, стоящее под знаком интеграла, будет равно нулю. Если выбрать такое направление обхода контура: a ® b ® c ® d ® а, то на участке ab направления векторов E_1t и dl совпадают, а на участке cd вектора E_2t и dl противоположны. Учитывая это, получаем:

,

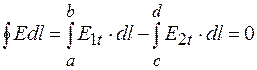поскольку длины участков ab и cd одинаковы по построению контура abcd, то следует:

Е_1t = E_2t, (1.40)

что и требовалось доказать.

При доказательстве второго утверждения будем использовать рис.1.5б. Если на поверхности раздела нет свободных зарядов, то их нет и в объеме прямоугольного параллелепипеда с бесконечно малой высотой, приведенного на рис.1.5б. Площадь верхней грани параллелепипеда (S₁) равна площади нижней грани (S₂) и обозначена символом S. Найдем поток нормальной составляющей вектора D (D_n) из объема параллелепипеда. Поток вектора D_n через каждую из четырех боковых поверхностей параллелепипеда равен нулю (см.§1.3). Поток вектора D_n через верхнюю грань Ф₁= D_1n×S₁ должен быть взят со знаком минус, поскольку направления векторов D_1n×и S₁ противоположны (поток входящий). Поток через нижнюю грань Ф₂= D_2n×S₂ берется со знаком плюс, поскольку направления векторов D_2n×и S₂ совпадают (поток выходящий). По теореме Остроградского – Гаусса полный поток из параллелепипеда равен нулю (свободных зарядов внутри нет):

Ф = Ф₁ + Ф₂ = D_2n×S – D_1n×S = 0,

откуда:

D_1n = D_2n, (1.41)

что и требовалось доказать. Если на поверхности раздела присутствуют свободные заряды, поток Ф не будет равняться нулю, а нормальная компонента вектора электрического смещения будет испытывать скачок, равный поверхностной плотности свободных зарядов s. Учитывая, что

D = e₀eE, из соотношения D_1n = D_2n получаем e₁×E_1n = e₂×E_2n, а из условия Е_1t = E_2t, следует D_1t/e₁ = D_2t/e₂. Эти соотношения можно переписать в виде:

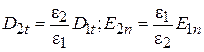(1.42)

Соотношения (1.40) ¸ (1.42) образуют правила преломления линий напряженности и электрического смещения электростатического поля на границе раздела двух диэлектриков. Учитывая, что tg(a₁) = E_1t/E_1n=D_1t/D_1n, tg(a₂) = E_2t/E_2n=D_2t/D_2n, и соотношения (1.40) ¸ (1.42) можно записать:

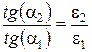. (1.43)

Проводящие включения в изоляцию

Проводники в электростатическом поле

Характерной особенностью проводников является наличие в них свободных электронов, которые могут перемещаться в пределах всего проводника. Из этого следует, что неподвижные свободные заряды одного и того же знака не могут сохраняться в толще проводника. Поскольку на заряды одного знака по закону Кулона действуют силы отталкивания, а сами заряды могут перемещаться в проводнике свободно, то они разойдутся на максимально возможное расстояние, которое определяется границами проводника, т.е. сосредоточатся на поверхности проводника. Объемная плотность заряда в толще проводника равна нулю.

Внутри проводника не может существовать и напряженность электростатического поля. Действительно, если бы такая напряженность существовала, то под ее действием возникло бы движение свободных электронов, т.е. ток, который продолжался бы до тех пор, пока не произошло бы такое перераспределение зарядов, при котором ток прекратится и установится равновесие, а напряженность станет равна нулю. Задача электростатики – задача о неподвижных зарядах, т.е. в рамках электростатики Е = 0 внутри проводника. По этой же причине Е = 0 и на поверхности проводника. Поскольку E = -grad(j) (см.1.7), то следует, что вся толща проводника, включая его поверхность, имеют одинаковый потенциал, т.е. являются эквипотенциальной областью. Это вывод следует подчеркнуть – поверхность проводника (электрода) - эквипотенциальная поверхность. Это значит, что напряженность поля у поверхности электрода имеет только нормальную составляющую напряженности, а тангенциальная равна нулю. По определению электрического смещения (1.22):

D = D_n = dq/ds = s =e₀eE_n; E_n = s/(e₀e), D_t =E_t = 0. (1.44)

Из (1.44) следует, что силовые линии электростатического поля диэлектрика изгибаются вблизи металлического включения таким образом, чтобы они были перпендикулярны поверхности металла.

Поле внутри полости проводника.

Электростатическое экранирование

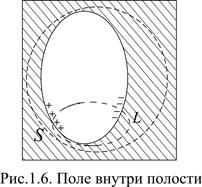Рассмотрим металлический проводник произвольной формы, имеющий внутри изолированную полость, в которой отсутствуют свободные заряды. В самом металле, как показано выше поля нет, но есть ли оно в полости? Покажем, что как бы ни был заряжен проводник, какова бы ни была его форма и форма полости, в каком бы электростатическом поле он ни находился, если полость пуста (т.е. в ней нет зарядов), то поле внутри полости будет равно нулю. Выберем произвольную замкнутую поверхность S, которая окружает полость и всюду лежит внутри проводника. Поскольку в любой точке проводника напряженность поля равна нулю, а любая точка произвольной поверхности S лежит внутри проводника, то поток вектора Е (D) равен нулю через любой элемент поверхности и общий поток вектора напряженности (электрического смещения) через всю поверхность S также будет равен нулю. По теореме Остроградского – Гаусса в этом случае суммарный заряд внутри объема, ограниченного поверхностью S, должен быть равен нулю. Зарядов внутри проводника, как показывалось выше, быть не может, внутри полости (по определению задачи) – тоже, но может они есть на внутренней поверхности полости? Если они там есть, но их сумма равна нулю, то полный поток сквозь поверхность S останется равным нулю и теорема Остроградского – Гаусса не будет нарушена. Предположим, что на внутренней поверхности полости имеется равное количество положительных и отрицательных зарядов. В таком случае внутри полости должны быть силовые линии, которые начинаются на положительных зарядах и заканчиваются на отрицательных зарядах. Выберем такую предполагаемую произвольную силовую линию и замкнем произвольный контур по толще проводника (контур L). Работа по перемещению пробного заряда вдоль этого контура внутри полости не равна нулю, если справедливо наше предположение о наличии зарядов на внутренней поверхности и напряженности поля в полости. Аналогичная работа по толще проводника равна нулю, поскольку вся толща проводника имеет одинаковый потенциал. В результате получается, что суммарная работа по замкнутому контуру L не равна нулю, что, понятно, противоречит определению электростатического поля. Следовательно, наше предположение о существовании зарядов на поверхности пустой полости не верно, т.е. вся внутренняя поверхность полости также представляет собой эквипотенциальную поверхность, а силовых линий поля в пустой полости быть не может. Это объясняет принцип «защиты» или «электростатического экранирования» оборудования, которое помещается в металлическую коробку. С помощью вышеприведенных рассуждений можно показать, что каким бы ни было распределение зарядов внутри полости, оно не может создать поле вне проводника. При практическом применении «электростатического экранирования» часто бывает достаточно окружить защищаемый объект не сплошным металлическим листом, а сеткой – экраном.

Распределение зарядов по поверхности проводника

Рассмотрим вопрос распределения зарядов по поверхности металлического проводника. Заряд распределяется по поверхности проводника равномерно с одинаковой поверхностной плотностью (s) в следующих случаях: а) на бесконечной заряженной плоскости, удаленной от других заряженных тел; б) на одиночном сферическом проводнике. Распределение заряда перестает быть равномерным, если размеры плоскости не бесконечны, форма проводника отличается от сферической или вблизи находятся другие заряженные тела. В следующем разделе будет показано, что напряженность поля пропорциональна квадрату радиуса кривизны поверхности. Напряженность резко возрастает на любых неровностях поверхности и на острых краях электродов. Этим объясняется явление истечения зарядов с острых краев электродов (кистевой разряд) и возникновение короны – ионизация и свечение газа под воздействием высокого напряжения («огни Святого Эльма»- корона на вершинах мачт). Эти явления приводят к потерям энергии на линиях электропередач и в аппаратах высокого напряжения.