Определение скоростей и ускорений структурных групп

3.5.1. Группа Ассура 1-го вида (рис. 3.7, а)

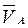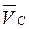Дано: скорости точек и . Определить: скорости точек 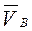, , 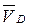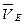; угловые скорости звеньев , .

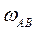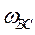Выразим скорость точки В в виде суммы векторов переносного и относительного движения

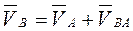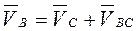; (3.31)

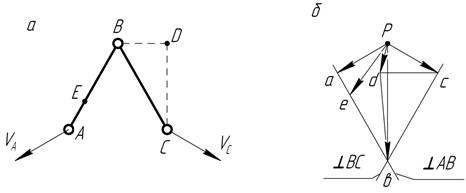
Рис. 3.7. Построение плана скоростей структурной группы 1-го вида.

Скорость точки В неизвестна ни по величине, ни по направлению. Относительные скорост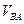и и 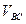неизвестны по величине, но известны по направлению: ; .

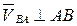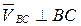Система векторных уравнений определима, если число уравнений равно числу неизвестных, умноженному на 2. Наша система содержит два векторных уравнения и четыре неизвестных, то есть является определимой.

Строим план скоростей (рис. 3.7, б). Откладываем произвольный отрезок ра в направлении вектора 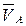, определяем масштабный коэффициент

.

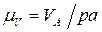С учетом масштабного коэффициента откладываем отрезок рс в направлении вектора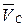

.

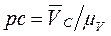Через точку а проводим прямую, перпендикулярную АВ, через точку с —прямую, перпендикулярную ВС. Точка пересечения этих прямых (направлений относительных скоростей) определяет общее решение двух уравнений (3.31).

Скорость точки D определяем по принципу подобия. Для этого строим на отрезке bс подобный и сходственный треугольник ( 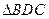~ 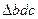). Соединяем полюс с точкой d и определяем скорость точки D

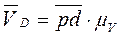
Скорость точки Е определяем также по принципу подобия

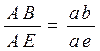(3.32)

отсюда

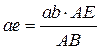(3.33)

Отложив на отрезке аb плана скоростей длину отрезка ае, со­единяем точку е с полюсом и определяем скорость точки Е:

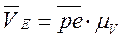
Далее определяем угловые скорости звеньев

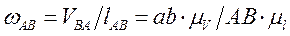
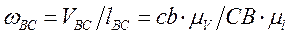(3.34)

где 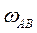— угловая скорость звена АВ;

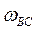— угловая скорость звена ВС;

АВ, ВС — отрезки на плане механизма, изображающие длины звеньев в масштабе;

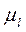— масштабный коэффициент длин.

Для того, чтобы определить направления угловых скоростей, векторы относительных скоросте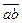й и 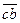следует мысленно перенести в точ­ку В плана механизма. Вектор относительной скорости 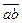вращает звено АВ по часовой стрелке, вектор 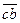вращает звено ВС против часовой стрелки (см. рис. 3.7).

Аналогичным образом строится план ускорений. Разница заклю­чается лишь в том, что относительные ускорения раскладываются на две составляющие: нормальную и касательную.

Дано: ускорения точек 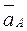, 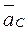(рис. 3.8, а). Известны все ско­рости, т. к. план скоростей уже построен (см. рис. 3.7, б).

Определить: ускорения точек 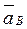, , 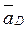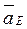; угловые ускорения звеньев , .

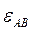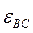Векторные уравнения для построения плана ускорений

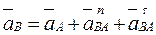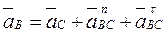; (3.35)

Векторы 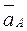, 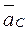известны по величине и направлению. Величину векторов 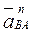, 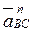можно определить, а направления их известны: 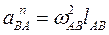; (вектор направлен от точки В к точке А);
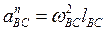(вектор направлен от точки В к точке С).

Касательные составляющие относительных ускорений известны только по направлению: , .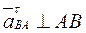

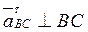Таким образом, имеется два векторных уравнения с четырьмя неизвестными, решая которые, определяем абсолютное ускорение .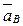

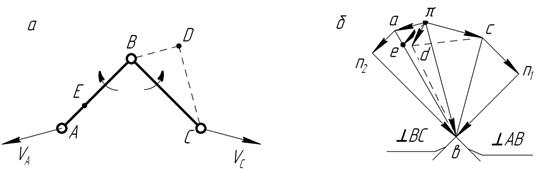
Рис. 3.8. Построение плана ускорений структурной группы 1-го вида

Из полюса 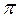(рис. 3.8, б) откладывается в направлении вектора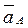

отрезок произвольной длины .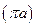

Определяем масштабный коэффициент плана ускорений

.

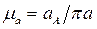С учетом масштаба строим все остальные векторы. Ускорение точки С — в виде отрезка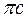

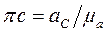, вектор πс направлен параллельно а_С .

Из точек а и с откладываем в масштабе векторы 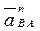и 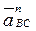параллельно отрезкам АВ и ВС, соответственно.

, .

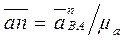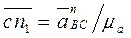Через точки n и n₁ проводим прямые, соответствующие направ­лениям касательных ускорений (через точку n — перпендикуляр к звену АВ, через точку n₁ — перпендикуляр к звену ВС).

Точка пересечения этих двух прямых определяет ускорение точки В

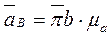
Ускорения точек D и Е определяются по правилу подобия; для этого на отрезке bc, изображающем полное относительное ускоре­ние 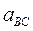строится треугольник bdc подобный и сходственный с тре­угольником BDC. Находим ускорение точки D

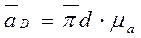
Из пропорционального деления отрезков определяют отрезок, изображающий ускорение точки Е:

,

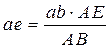а затем длину отрезка πе умножают на масштабный коэффициент

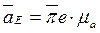
Величину и направления угловых ускорений находят по касательным составляющим относительных ускорений (см. рис. 3.8, б)

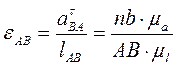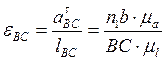; (3.36)

Направления угловых ускорений звеньев определяют, мысленно перенося векторы 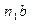и nb с плана ускорений в точку В. Первый вектор вращает звено ВС против часовой стрелки, второй вращает звено АВ по часовой стрелке. Направления угловых ускорений показаны круговыми стрелками (см. рис. 3.8,а).