Группа Ассура 3-го вида

Построение планов скоростей и ускорений рассмотрим на при­мере кулисного механизма, который образован присоединением к механизму I класса группы Ассура II класса 3-го вида (рис. 3.10).

Дано: кинематическая схема механизма; угловая скорость кривошипа .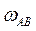

Определить: скорость и ускорение точек В' и D кулисы; угловую скорость и угловое ускорение кулисы.

Строим план скоростей (рис. 3.10, б) по векторному уравне­нию

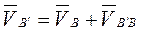
где 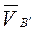— скорость точки В', принадлежащей кулисе;

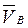— скорость точки В конца кривошипа и кулисного камня;

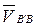— относительная, скорость движения камня по кулисе.

;

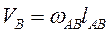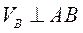
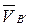перпендикулярна кулисе DC ; 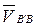параллельна DC.

Имеем одно векторное уравнение с двумя неизвестными: величиной V_В' и величиной V_В'В . Перпендикулярно радиусу вращения (длине кривошипа) АВ откладываем отрезок произвольной величины, изображающий известную скорость 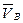. Масштабный коэффи­циент плана скоростей .

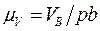Через точку b проводим направление относительной скорости (параллельно кулисе DC); через полюс — направление абсолютной скорости точки В' (перпендикулярно кулисе). Точка пересечения определяет скорость точки В' кулисы

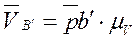
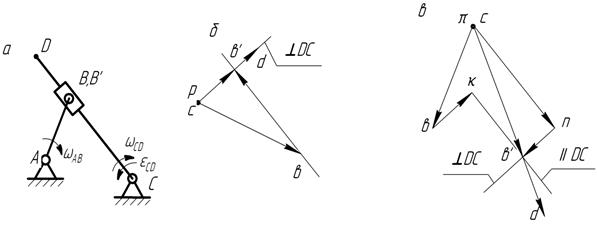
Рис. 3.10. Пример построения плана скоростей и ускорений структурной группы 3-го вида: а — план механизма; б — план скоростей; в — план ускорений.

Скорость точки D находим по принципу подобия: строим на плане скоростей отрезок pd, пропорциональный длине кулисы CD

.

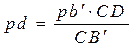Абсолютная скорость точки D определяется отрезком pd с учетом масштабного коэффициента .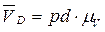

Угловая скорость кулисы 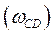определится из соотношения

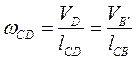
Направление угловой скорости находим, мысленно перенося вектор относительной скорости с плана скоростей в соответствующую точку механизма. Кулиса вращается по часовой стрелке (см. рис. 3.10, а, б).

План ускорений строим по векторному уравнению

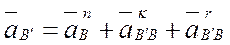
где 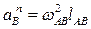- нормальное ускорение переносного движения (ускорение точки В конца кривошипа и кулисного камня). Вектор нормального ускорения направлен параллельно АВ от точки В к точке А. Откладываем в этом направлении отрезок произвольной величи­ны (рис. 3.10, в) и определяем масштабный коэффициент плана ускорений

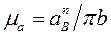
Второй член уравнения — Кориолисово ускорение, вычисляем его по формуле:

,

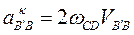где 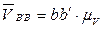(см. рис. 3.10, б).

Направление Кориолисова ускорения определяем поворотом век­тора относительной скорости (bb' — на плане скоростей) на 90° в направлении угловой скорости кулисы 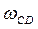. Из точки b (рис. 3.10, б) откладываем
в масштабе величину Кориолисова ускорения

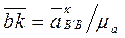
Через точку k проводим параллельно СD направление релятивного ускорения. Величина этого ускорения неизвестна, поэтому требуется составить еще одно векторное уравнение. Кулиса вращается нерав­номерно, поэтому ускорение точки В во вращательном движении вокруг точки С складывается из нормального и касательного

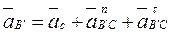
где 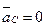, так как С — неподвижная точка, и ее ускорение изображается на плане нулевым отрезком (совпадает с полюсом).

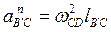; вектор направлен параллельно ВʹС.

Откладываем в направлении от В' к С отрезок, изображающий нормальную составляющую ускорения (см. рис. 3.10, в):

.

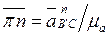Через точку n проводим направление касательного ускорения (перпендикулярно кулисе). Получаем точку пересечения b', которая определяет ускорение точки В' кулисы

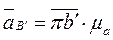
Ускорение точки D находим по принципу подобия

; .

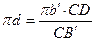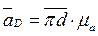Угловое ускорение кулисы определяем по касательной состав­ляющей 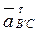, которая на плане ускорений изображается отрезком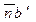

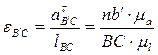
Направление углового ускорения находим, перенося вектор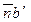
(рис. 3.10, в) в точку В' кулисы (рис. 3.10, а). Угловое ускорение направлено против часовой стрелки.