Задачи и методы кинематического анализа
Основным назначением механизма является выполнение требуемых движений, которые описываются с помощью кинематических характеристик.
Кинематический анализ — это изучение движения звеньев механизма без учета действующих сил.
Под кинематическими характеристиками понимаются перемещения, скорости и ускорения точек, а также угловые скорости иугловые ускорения звеньев. Определение траекторий точек необходимо для того, чтобы спроектировать, например, корпус машины, очертания картеров, исключить столкновение звеньев при движении и т. д. Кроме того, кинематический анализ дает возможность перейти к следующему этапу проектирования — динамическому расчету, при котором необходимо знать скорости иускорения точек и звеньев.
Перемещения, скорости, ускорения определяют в пределах цикла работы механизма, т. е. за один оборот ведущего звена, для нескольких положений. Движение звеньев зависит от закона движения ведущего звена, поэтому при решении задач кинематического анализа должны быть заданы:
1) структурная схема механизма с указанием ее размеров
(т. е. кинематическая схема);
2) закон движения начального звена.
Основные методы кинематического анализа:
— метод построения планов;
— метод кинематических диаграмм;
— аналитический метод.
Используя принципы структурного анализа, т. е. разложения механизма на группы Ассура, можно применять методы кинематического исследования не ко всему механизму в целом, а к отдельным частям его, что упрощает задачу.
Графические методы отличаются простотой и наглядностью, иногда они являются единственно приемлемыми, т. к. дают наиболее простое решение. Если же требуется провести большой объем однообразных построений, а также в том случае, когда необходимо провести расчеты с высокой точностью, целесообразно использовать аналитические методы.
Планы положений механизма
Изображение кинематической схемы механизма, соответствующее определенному положению начального звена, называется планом механизма. Планы строятся в заданном масштабе. При этом различают понятия масштаб и масштабный коэффициент. Масштабом физической величины называют длину отрезка в миллиметрах, изображающую единицу измерения этой величины. Масштабным коэффициентом физической величины называют отношение численного значения физической величины к длине отрезка в миллиметрах, изображающего эту величину. Масштаб и масштабный коэффициент являются взаимнообратными величинами. Масштабные коэффициенты обозначают буквой 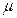 с индексом, указывающим, к какой величине они относятся. Например, масштабный коэффициент длин
с индексом, указывающим, к какой величине они относятся. Например, масштабный коэффициент длин 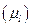 для плана механизма есть отношение какой-либо длины
для плана механизма есть отношение какой-либо длины 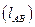 в метрах к отрезку
в метрах к отрезку 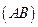 , изображающему эту длину на чертеже в миллиметрах:
, изображающему эту длину на чертеже в миллиметрах:
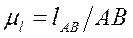
Рассмотрим построение планов механизма на примерах.
1. Шарнирный четырехзвенник (рис. 3.1). Кривошип ОА вращается с постоянной скоростью ωо , поэтому положение точки А известно для любого момента времени (любого угла поворота звена ОА).
Делим окружность радиуса ОА на несколько равных частей, например,
на 6. Обозначим положения конца кривошипа точками 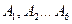 .
.
Точка В (конец коромысла) движется по дуге окружности радиуса СВ. Проведем эту дугу из центра — точки С.
Радиусом, равным длине шатуна АВ, делаем из точек 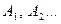 засечки на дуге окружности В1, В2, …и т.д .
засечки на дуге окружности В1, В2, …и т.д .
Соединяем одноименные положения точек 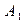 и
и 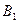 ,
, 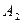 и
и 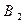 , а также
, а также 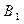 и
и 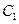
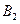 и
и 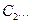 Получаем положения шатуна и коромысла за цикл движения,
Получаем положения шатуна и коромысла за цикл движения,
т. е. за один оборот кривошипа. Вращение коромысла против часовой стрелки соответствует положениям рабочего хода, по часовой стрелке — положениям холостого хода.
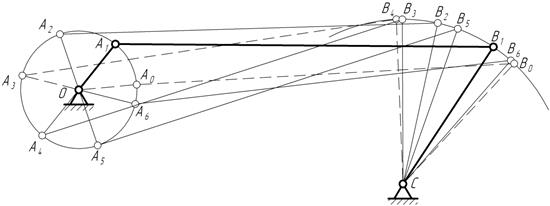
Рис. 3.1. Построение плана положений шарнирного четырехзвенника
2. Кривошипно-ползунный механизм (рис. 3.2). Задаемся крайним положением кривошипа (кривошип и шатун располагаются на одной линии).
Делим окружность радиуса ОА на равные части. Из точек деления 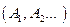 делаем засечки на оси движения ползуна
делаем засечки на оси движения ползуна 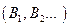 радиусом, равным длине шатуна. Найденные положения точки В определяют положение поршня (ползуна): на рабочем ходу
радиусом, равным длине шатуна. Найденные положения точки В определяют положение поршня (ползуна): на рабочем ходу 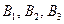 ; на холостом ходу -
; на холостом ходу - 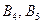 . Соединяем одноименные точки
. Соединяем одноименные точки 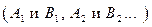 .
.
Рис. 3.2. Построение плана положений кривошипно-ползунного механизма
Планы скоростей плоских механизмов
Планом скоростей называют чертеж, на котором изображены в виде отрезков векторы, равные по модулю и по направлению скоростям различных точек механизма в данном положении.
Для построения плана скоростей необходимы исходные данные:
1) план механизма с указанием размеров;
2) угловая скорость начального звена.
Из теоретической механики известно, что любое движение плоского тела может рассматриваться как сумма двух движений: вращение относительно некоторой точки (полюса) и поступательное (переносное) движение полюса. Используя этот принцип, рассмотрим решение задач о скоростях точек звеньев, образующих пары 5-го класса.
Задача 1. Определение скоростей точек звена, входящего во вращательную пару с другим звеном.
Пусть заданы: 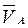 - вектор скорости точки A (рис. 3.3, а);
- вектор скорости точки A (рис. 3.3, а);
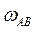 - угловая скорость звена АВ. Требуется определить: скорости точек В и С
- угловая скорость звена АВ. Требуется определить: скорости точек В и С 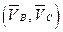 .
.

|
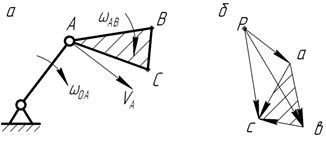
Рис. 3.3. Построение плана скоростей точек звена, входящего во вращательную пару с другим звеном
В соответствии с теоремой сложения скоростей абсолютная скорость 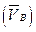 точки равна геометрической сумме переносной
точки равна геометрической сумме переносной 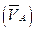 и относительной
и относительной 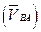 скоростей этой точки
скоростей этой точки
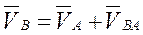 , (3.1)
, (3.1)
где 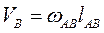 - относительная скорость точки В во вращательном движении вокруг точки А;вектор
- относительная скорость точки В во вращательном движении вокруг точки А;вектор 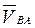 направлен перпендикулярно звену АВ (т.е. радиусу вращения). Аналогично
направлен перпендикулярно звену АВ (т.е. радиусу вращения). Аналогично
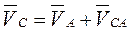 , (3.2)
, (3.2)
где 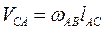 ; вектор этой скорости направлен перпендикулярно звену
; вектор этой скорости направлен перпендикулярно звену 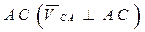 .
.
Построим векторные уравнения (3.1) и (3.2).
1. Выбираем произвольную точку р - полюс плана скоростей и откладываем в направлении вектора 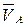 отрезок произвольной длины ра
отрезок произвольной длины ра
(рис. 3.3, б). При этом определяем значение масштабного коэффициента плана скоростей
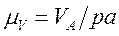 (3.3)
(3.3)
2. Строим вектор 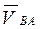 . Из точки а проводим прямую, перпендикулярную стороне звена АВ и откладываем отрезок ab в масштабе, учитывая направление угловой скорости
. Из точки а проводим прямую, перпендикулярную стороне звена АВ и откладываем отрезок ab в масштабе, учитывая направление угловой скорости 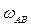 :
:
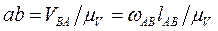 . (3.4)
. (3.4)
3. Суммарный вектор - абсолютная скорость точки В - определится отрезком рb
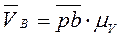 . (3.5)
. (3.5)
4. Аналогично находим скорость точки С: из точки а в направлении, перпендикулярном стороне звена АС, откладываем относительную скорость
с учетом масштабного коэффициента
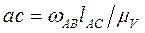 . (3.6)
. (3.6)
Соединяем полюс с полученной на плане скоростей точкой С. Измерив на плане величину отрезка рс, находим значение абсолютной скорости точки С:
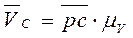 . (3.7)
. (3.7)
5. Скорость точки С можно определить, приняв движение точки В за переносное:
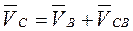 . (3.8)
. (3.8)
На плане скоростей (см. рис. 3.3, б) вектор 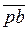 изображает скорость точки В; относительная скорость
изображает скорость точки В; относительная скорость 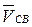 - это вектор
- это вектор 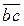 , направленный перпендикулярно стороне звена ВС (см. рис. 3.3, а). Соединив точки b и с, получим на плане скоростей графическое изображение уравнения (3.8).
, направленный перпендикулярно стороне звена ВС (см. рис. 3.3, а). Соединив точки b и с, получим на плане скоростей графическое изображение уравнения (3.8).
Сравнивая треугольники ABC и abc на рис. 3.3, можно заметить, что эти фигуры подобны и сходственны, поскольку стороны их взаимно перпендикулярны и отрезки ab, ас, bс пропорциональны длинам сторон звена АВ, АС, ВС.
ВЫВОДЫ
На плане скоростей лучи, выходящие из полюса, изображают абсолютные скорости точек звена, а отрезки, соединяющие концы лучей — относительные скорости соответствующих точек.
Векторы относительных скоростей направлены на плане скоростей к первой букве индекса. Например, 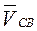 - скорость точки С относительно В.
- скорость точки С относительно В.
На плане скоростей читается наоборот: отрезок 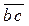 , но вектор направлен к точке с.
, но вектор направлен к точке с.
3. Векторы относительных скоростей точек жесткого звена образуют на плане скоростей фигуру, подобную этому звену, повернутую на 90° в направлении угловой скорости звена.
Последний вывод называется принципом подобия в плане скоростей и позволяет определить скорость любой точи звена графически, если известны скорости хотя бы двух точек этого звена.
Задача 2. Определение скоростей точек звена, входящего в поступательную пару.
Пусть заданы: 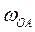 - угловая скорость звена О А (рис. 3.4 а);
- угловая скорость звена О А (рис. 3.4 а);
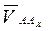 - скорость звена АВ относительно направляющей х — х.
- скорость звена АВ относительно направляющей х — х.
Требуется определить: скорость точки 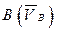 , лежащей на звене АВ.
, лежащей на звене АВ.
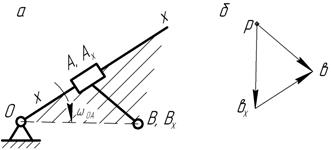
Рис. 3.4. Построение плана скоростей точек звена, входящего в поступательную пару
Точки А и 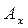 совпадают, но принадлежат разным звеньям: А - звену АВ;
совпадают, но принадлежат разным звеньям: А - звену АВ; 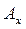 - звену ОА (или направляющей х — х). То же самое можно сказать о точках В и Вx . Тогда скорость точки В определяется уравнением
- звену ОА (или направляющей х — х). То же самое можно сказать о точках В и Вx . Тогда скорость точки В определяется уравнением
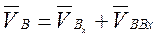 (3.9)
(3.9)
где 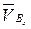 — скорость переносного движения (точки В, принадлежащей направляющей);
— скорость переносного движения (точки В, принадлежащей направляющей); 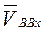 — скорость относительного движения (точки В относительно
— скорость относительного движения (точки В относительно 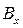 ). Поскольку звено АВ движется поступательно относительно направляющей х— х, то справедливо равенство:
). Поскольку звено АВ движется поступательно относительно направляющей х— х, то справедливо равенство:
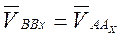 (3.10)
(3.10)
Переносная скорость определяется из выражения
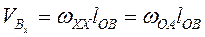 (3.11)
(3.11)
где 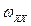 — угловая скорость вращения направляющей x — x.
— угловая скорость вращения направляющей x — x.
Вектор 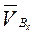 откладываем из полюса перпендикулярно ОВ в виде отрезка
откладываем из полюса перпендикулярно ОВ в виде отрезка
произвольной длины 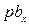 . Определяем масштабный коэффициент
. Определяем масштабный коэффициент
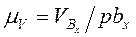 (3.12)
(3.12)
Вектор 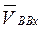 откладываем с учетом масштабного коэффициента в направлении, параллельном х — х (рис. 3.4, б ) в виде отрезка
откладываем с учетом масштабного коэффициента в направлении, параллельном х — х (рис. 3.4, б ) в виде отрезка
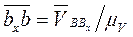 (3.13)
(3.13)
Скорость точки В определяется сложением векторов 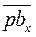 и
и 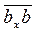
(см. рис. 3.4, б). Получаем вектор 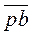 , который затем умножается
, который затем умножается
на масштабный коэффициент
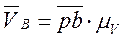 (3.14)
(3.14)
Планы ускорений плоских механизмов
Чертеж, на котором изображены в виде отрезков векторы, равные по модулю и направлению ускорениям различных точек звеньев механизма в данном положении, называется планом ускорений.
Рассмотрим решение двух задач об определении ускорений точек звеньев, образующих кинематические пары 5-го класса, аналогично решению задач о скоростях (см. раздел 3.3).
Задача 1. Ускорение точек звена, входящего во вращательную пару.
При построении плана ускорений считается, что все скорости известны,
т. е. план скоростей механизма для данного положения уже построен.
Пусть заданы: 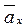 —ускорение точки А;
—ускорение точки А; 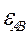 — угловое ускорение звена ABC.
— угловое ускорение звена ABC.
Требуется определить: ускорения точек В и С 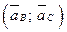 .
.
Абсолютное ускорение точки В складывается из переносного ускорения 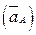 и относительного ускорения
и относительного ускорения 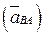 во вращательном движении точки В вокруг А (рис. 3.5, а):
во вращательном движении точки В вокруг А (рис. 3.5, а):
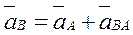 (3.15)
(3.15)
Поскольку относительное движение вращательное, неравномерное, то, как известно из теоретической механики, ускорение складывается из нормального и касательного
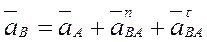 (3.16)
(3.16)
где 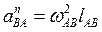 — нормальное ускорение в относительном движении, направленное по радиусу вращения AВ к центру вращения (точке А);
— нормальное ускорение в относительном движении, направленное по радиусу вращения AВ к центру вращения (точке А);
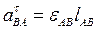 — касательное ускорение в относительном движении, направленное перпендикулярно радиусу вращения АВ.
— касательное ускорение в относительном движении, направленное перпендикулярно радиусу вращения АВ.
Построим уравнение (3.16) в виде суммы векторов (рис. 3.5, б)
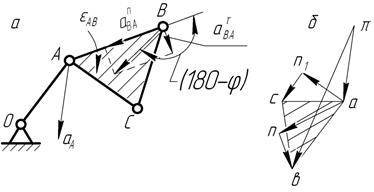
Рис. 3.5. Построение плана ускорений точек звена, входящего во вращательную пару.
Выбираем точку π — полюс плана ускорений. Откладываем из полюса вектор 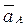 в виде отрезка произвольной длины
в виде отрезка произвольной длины 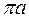 , направленного параллельно вектору
, направленного параллельно вектору 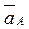 . Определяем масштабный коэффициент
. Определяем масштабный коэффициент
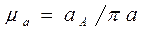 (3.17 )
(3.17 )
Из точки а откладываем в направлении к центру вращения с учетом масштаба отрезок an, изображающий вектор нормального ускорения. Величина отрезка an определяется соотношением:
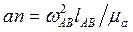 (3.18)
(3.18)
От полученной точки п в направлении, перпендикулярном АВ, откладываем отрезок nb, изображающий в масштабе касательную составляющую относительного ускорения:
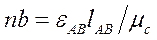 (3.19)
(3.19)
Направление вектора 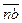 определяется с учетом направления углового ускорения
определяется с учетом направления углового ускорения 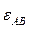 (в данном примере — вниз). Соединяя точку π с точкой b, получаем результирующий вектор, который изображает абсолютное ускорение точки В (см. уравнение 3.16).
(в данном примере — вниз). Соединяя точку π с точкой b, получаем результирующий вектор, который изображает абсолютное ускорение точки В (см. уравнение 3.16).
Величину абсолютного ускорения точки В находим через масштабный коэффициент
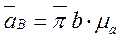 (3.20)
(3.20)
Аналогично строятся векторные уравнения для точки С (см. рис. 3.5)
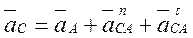 (3.21)
(3.21)
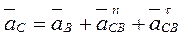 (3.22)
(3.22)
Определим значения полных относительных ускорений
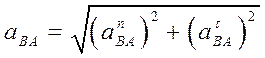 (3.23)
(3.23)
С учетом известных из теоретической механики формул (см. значения величин, входящих в уравнение (3.16)), получим
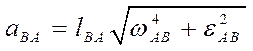 (3.23.1)
(3.23.1)
Аналогично:
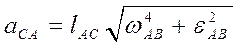 (3.23.2)
(3.23.2)
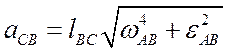 (3.23.3)
(3.23.3)
Тангенс угла, определяющего направление полного относительного ускорения, (см. рис. 3.5, а):
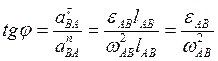 (3.24)
(3.24)
Из формулы (3.24) следует, что тангенс угла 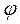 не зависит от того, какая точка звена рассматривается и одинаков для всех относительных ускорений.
не зависит от того, какая точка звена рассматривается и одинаков для всех относительных ускорений.
Из выражений (3.23.1), (3.23.2), (3.23.3), (3.24) следует, что относительные ускорения точек звена ABC пропорциональны длинам сторон и повернуты на один и тот же угол. Следовательно, 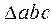 в плане ускорений и
в плане ускорений и 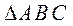 (жесткое звено) подобны между собой и сходственны. Этим определяется принцип подобия в плане ускорений.
(жесткое звено) подобны между собой и сходственны. Этим определяется принцип подобия в плане ускорений.
ВЫВОД: Векторы относительных ускорений точек жесткого звена образуют на плане ускорений фигуру, подобную этому звену и повернутую относительно него на угол (180°— 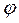 ) в направлении углового ускорения.
) в направлении углового ускорения.
Зная относительные ускорения хотя бы двух точек звена, можно определить ускорение любой точки этого звена, пользуясь принципом подобия.
Задача 2. Ускорение точек звена, входящего в поступательную пару.
Пусть заданы:
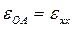 - угловое ускорение звена ОА, т. е. направляющей х — х (рис. 3.6, а);
- угловое ускорение звена ОА, т. е. направляющей х — х (рис. 3.6, а);
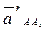 — ускорение звена АВ в относительном поступательном движении
— ускорение звена АВ в относительном поступательном движении
(так называемое, релятивное ускорение).
Требуется определить: ускорение точки В звена АВ.
Точки А, 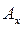 совпадают, но принадлежат разным звеньям: А — звену АВ,
совпадают, но принадлежат разным звеньям: А — звену АВ,
 — звену ОА (то есть направляющей x – x).
— звену ОА (то есть направляющей x – x).
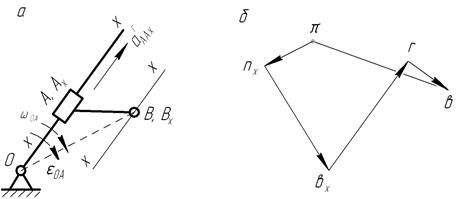
Рис. 3.6. Построение плана ускорений точек звена, входящего в поступательную пару
Абсолютное ускорение точки В складывается из переносного ускорения точки Вх , которая принадлежит направляющей х - x и движется по окружности радиуса ОВ, относительного ускорения точки B в поступательном движении звена АВ вдоль направляющей х - x и Кориолисова (поворотного) ускорения.
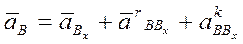 (3.25)
(3.25)
Переносное движение - вращательное, неравномерное, поэтому ускорение складывается из нормального и касательного
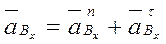 (3.26 )
(3.26 ) 
Величина и направление составляющих переносного ускорения определяются по известным из теоретической механики формулам
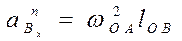 (3.26.1)
(3.26.1)
Вектор 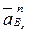 направлен параллельно ОВ к центру вращения - точке О.
направлен параллельно ОВ к центру вращения - точке О.
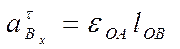 (3.26.2)
(3.26.2)
Вектор 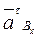 направлен перпендикулярно ОВ.
направлен перпендикулярно ОВ.
Относительное движение - поступательное, поэтому все точки движутся с одинаковым ускорением
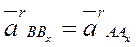 (3.27)
(3.27)
Составляющая Кориолисова ускорения обусловлена приращением вектора переносной скорости вследствие изменения длины радиуса вращения 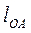 , а также поворотом вектора относительной скорости. Согласно правилу Жуковского для плоского движения направление Кориолисова ускорения определяется поворотом вектора относительной скорости на 90° в направлении переносной угловой скорости, а величина его рассчитывается по формуле:
, а также поворотом вектора относительной скорости. Согласно правилу Жуковского для плоского движения направление Кориолисова ускорения определяется поворотом вектора относительной скорости на 90° в направлении переносной угловой скорости, а величина его рассчитывается по формуле:
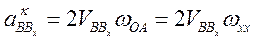 (3.28)
(3.28)
Таким образом, чтобы определить полное (то есть абсолютное) ускорение точки В, необходимо сложить четыре вектора:
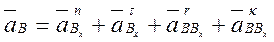 (3.29)
(3.29)
Согласно рассмотренным в предыдущих разделах правилам, строят план ускорений (рис. 3.6, б).
Отрезок 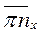 изображает ускорение
изображает ускорение 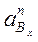 Величина его выбирается произвольно, после чего рассчитывается масштабный коэффициент
Величина его выбирается произвольно, после чего рассчитывается масштабный коэффициент
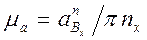 (3.30)
(3.30)
Отрезки 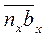 ,
, 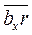 ,
, 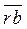 изображают соответственно ускорения
изображают соответственно ускорения 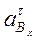 ,
,
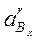 ,
, 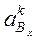 с учетом принятого масштабного коэффициента
с учетом принятого масштабного коэффициента 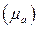 . Величины отрезков на плане ускорений составят, соответственно:
. Величины отрезков на плане ускорений составят, соответственно:
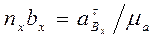
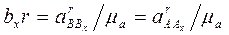
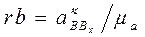
Направления векторов: нормального ускорения 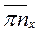 - параллельно ВО, к центру вращения; касательного ускорения
- параллельно ВО, к центру вращения; касательного ускорения 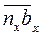 - перпендикулярно ВО с учетом направления углового ускорения;
- перпендикулярно ВО с учетом направления углового ускорения; 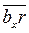 - задано исходными данными (параллельно кулисе);
- задано исходными данными (параллельно кулисе); 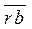 - определяется правилом Жуковского.
- определяется правилом Жуковского.
Соединив точку π с точкой b, получаем вектор 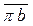 изображающий в масштабе абсолютное ускорение точки В:
изображающий в масштабе абсолютное ускорение точки В:
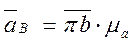
Последовательно переходя от начального звена к 1-й группе Ассура, затем к следующей и т. д., можно определить скорости и ускорения всех точек и звеньев механизма.
Дата добавления: 2020-12-11; просмотров: 1166;











