Аналоги скоростей и ускорений

Во многих случаях при проектировании машин и механизмов законы движения звеньев в функции времени можно определить только на последующих стадиях проектирования, обычно после динамического анализа с учетом приложенных сил [2, с. 61].

В таких случаях движение звеньев определяется в два этапа: сначала устанавливаются зависимости кинематических параметров в функции обобщенной координаты (угла поворота ведущего звена), а затем определяется закон изменения обобщенной координаты во времени. Для выполнения подобных расчетов вводятся понятия аналогов скоростей и ускорений.

Аналогом скорости какой-либо точки называется первая производная радиус-вектора этой точки по обобщенной координате. Для поступательного движения перемещение точки можно считать равным радиус-вектору. Тогда аналог скорости согласно определению

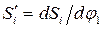(3.37)

где 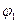- обобщенная координата (угол поворота звена 1);

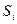- перемещение точки i-ro звена.

Скорость данной точки 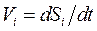, поэтому

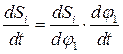(3.38)

Учитывая формулу (3.37), получаем связь между истинной ско­ростью и ее аналогом:

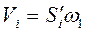(3.39)

где 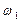- угловая скорость начального звена.

Физический смысл аналога скорости - это скорость той же точки при 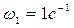; единица измерения аналога скорости - метр.

Аналогом ускорения точки называется вторая производ­ная радиус-вектора точки по обобщенной координате.

Чтобы установить связь ускорения с аналогом ускорения продифференцируем (3.39) по времени

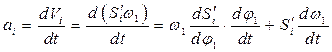(3.40)

Окончательно получим

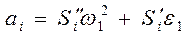(3.41)

где 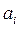- ускорение точки i-го звена;

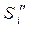- аналог ускорения той же точки;

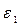- угловое ускорение начального звена.

При вращательном движении звена вводятся понятия анало­гов угловых скоростей и ускорений.

Аналогом угловой скорости называется первая про­изводная от угла поворота по обобщенной координате механизма

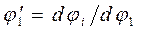, (3.42)

Где 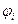- угол поворота i-го звена.

Угловая скорость звена 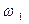связана с ее аналогом соотношением:

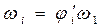(3.43)

Аналогом углового ускорения называется вторая производная от угла поворота звена по обобщенной координате механизма. Дифференцируя (3.43) по времени, получим

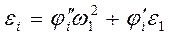(3.44)

Из формул (3.43) и (3.44) видно, что аналоги угловых скоро­стей и угловых ускорений являются безразмерными величинами.

3.7. Графическое дифференцирование и интегрирование как
метод кинематического анализа

Графическое изображение изменения основных кинематических параметров механизма за полный цикл движения называется кинематической диаграммой.

Если одна из кинематических функций задана в форме графика или в виде таблицы значений, то найти производную или интеграл от этой функции непосредственно в аналитической форме невозможно. В этом случае используют методы графического дифференцирования и интегрирования.

Основное достоинство данного метода, как и у большинства графических методов, - это наглядность и простота; недостаток - невысокая точность по сравнению с аналитическими методами. Метод основан на геометрическом смысле производной, которая представляет собой тангенс угла наклона касательной в данной точке кривой к оси абсцисс.

Обычно кривую заменяют ломаной линией и принимают следующее допущение: угол наклона касательных в точках, расположенных посередине каждого участка кривой, равен углу наклона соответствующей хорды. Это вносит некоторую погрешность, но она не суммируется, что обеспечивает приемлемую точность метода [2, с. 110].

На рис. 3.11 изображена кинематическая диаграмма перемещений точки в масштабе. Пусть за бесконечно малый промежуток времени Δtперемещение точки увеличилось на ΔS.Тогда скорость точки на этом участке определится из выражения

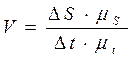(3.45)

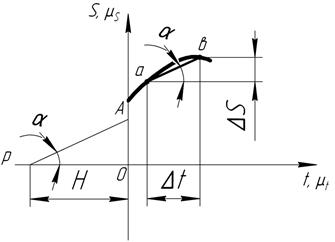
Рис. 3.11. К определению кинематических параметров методом кинематических диаграмм.

Из чертежа (см. рис. 3.11) следует, что ΔS/Δt=tgα , а с учетом принятого допущения это и есть первая производная (в пределе хорда превратится в касательную). Поэтому

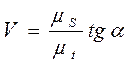(3.46)

Проведем из точки Р, расположенной влево от оси абсцисс на произвольном расстоянии Н, прямую, параллельную хорде ab, до пересечения с осью ординат. Эта прямая отсекает на оси ординат отрезок ОА, длина которого определяется из треугольника АОР

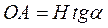(3.47)

Разделив (3.46) на (3.47), получим

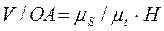(3.48)

Правая часть уравнения содержит только постоянные величи­ны, следовательно, она является также величиной постоянной и представляет собой масштабный коэффициент скоро­сти.

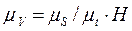(3.49)

Таким образом, отрезок ОА, отсекаемый лучом РА на оси ординат, изображает скорость на бесконечно малом участке Δt в масштабе скоростей μ_V.

3.8. Метод кинематических диаграмм