Кинематическая цепь. Структурная формула кинематической цепи.

Структура механизма определяется его кинематической цепью. Кинематическая цепь — это система звеньев, образующих меж­ду собой кинематические пары. Кинематические цепи различают но следующим признакам (рис. 1.3):

а) замкнутые и незамкнутые;

б) простые и сложные;

в) плоские и пространственные.

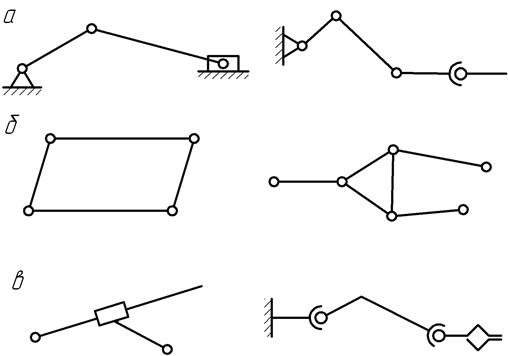
Рис. 1.3. Классификация кинематических цепей

В замкнутой цепи каждое звено входит не менее чем в две кинематические пары; в незамкнутой цепи есть звенья, входящие толь­ко в одну кинематическую пару.

В простой цепи каждое звено входит не более чем в две ки­нематические пары; в сложной цепи есть звенья, входящие более чем в две кинематические пары.

В плоской цепи все звенья перемещаются в одной, плоскости, либо в параллельных плоскостях; в пространственной - звенья движутся в разных, непараллельных плоскостях.

Кинематическая цепь характеризуется числом степеней свободы, равным числу входных звеньев.

Пусть в механизме имеется n подвижныхзвеньев. Каждое звено до соединения его с другим звеном имеет в пространстве 6 степеней свободы. Тогда общее число степеней свободы кинематической цепи равно 6n.

Соединение звеньев в кинематические пары накладывает определенное число связей, которые надо исключить из общего чис­ла степеней свободы.

Учитывая, что каждая пара 5-го класса накладывает 5 связей, пара 4-го класса — 4 связи и т. д., число степеней свободы механизма относительно стойки (неподвижного звена) определится по формуле:

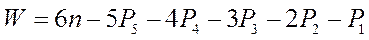(1.1)

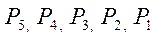— число кинематических пар 5-го, 4-го... 1-го класса.

Полученная формула называется структурной формулой кинематической цепи и носит имя А. П. Малышева.

Все механизмы классифицируются по семействам. Класс се­мейства определяется числом общих связей, наложенных на механизм. Если наложить на механизм одну общую связь, то по­лучим механизм 1-го семейства, и формула (1.3) примет вид

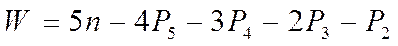(1.2)

Аналогично, если наложить 2 общие связи

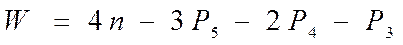(1.3)

Если наложить 3 общие связи, получим механизм 3-го семейства - плоский механизм. Из определения плоских механизмов следует, что у них из шести независимых движений (см. рис. 1.1) возможны только три: поступательное вдоль осей x и y, а также вращение относительно оси Z. При этом звенья будут двигаться в плоскости xОy.

Структурная формула кинематической цепи в этом случае принимает вид

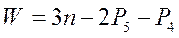(1.4)

и называется формулой Чебышева для плоских механизмов.