Замена высших кинематических пар низшими

В плоских механизмах все пары 4-го класса являются высшими, а пары
5-го класса - низшими. Поэтому формулу Чебышева можно представить в виде:

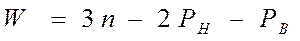(1.5)

n — число подвижных звеньев;

p_н— число низших кинематических пар;
pв — число высших кинематических пар.

При структурном анализе плоских механизмов высшие пары можно заменить низшими. Рассматривать механизмы с низшими парами удобнее, т. к. для них решены все основные задачи ана­лиза механизмов.

При замене высших пар на низшие должны выполняться следу­ющие условия:

1) степень подвижности механизма должна оставаться неиз­менной;

2) относительное движение звеньев также должно сохраняться.
Пусть для кинематической цепи, содержащей высшие и низшие кинематические пары, степень подвижности равна Wo.

Если убрать из кинематической цепи пару 4-го класса, то число степеней сво­боды станет на единицу больше, т. к. пара 4-го класса в плоском механизме накладывает одну связь (три общих связи уже наложено).

Вместо отброшенной пары необходимо приложить кинемати­ческую цепь, содержащую только низшие пары.

Тогда, чтобы выполнить 1-е условие, необходимо соблюсти равенство:

(1.6)

W₀- степень подвижности исходной цепи;

(W₀ + 1) - степень подвижности цепи с отброшенной высшей
парой;

(3n – 2 p₅) - степень подвижности цепи замены (содержащей только низшие пары).

Преобразуем равенство (1.6)

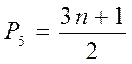(1.7)

Полученное выражение устанавливает соотношение между чис­лом звеньев и числом кинематических пар 5-го класса в цепи за­мены.

Учитывая, что p₅ и n - целые числа, определяется минималь­ное число звеньев и кинематических пар в цепи замены:

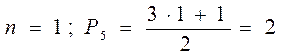
Вывод: высшую пару в кинематической цепи можно заменить дополнительным звеном и двумя низшими парами.

Пример. Имеется механизм, состоящий из звеньев 1 и 2 (рис.1.4).Контакт между звеньями - в точке, которая представляет собой высшую пару; А и В - низшие пары (вращательные); О₁и О₂ — центры кривизны звеньев.

Для замены высшей кинематической пары (рис. 1.4, а) про­водим нормаль в точке касания звеньев до центров кривизны О₁и О₂ (пунктирная линия). Соединяя точки О₁и О₂ с точками А и В, получим шарнирный четырехзвенник, у которого все пары низшие. Таким образом, высшую пару (точку касания звеньев) заменили дополнительным звеном 3и двумя низшими парами О₁и О₂ (рис. 1.4, б).

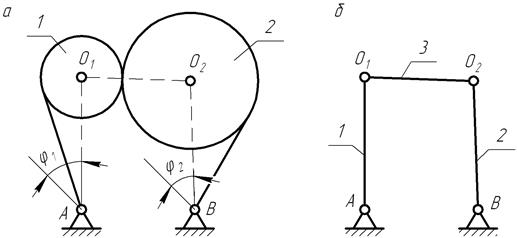
Рис 1.4. Замена высшей пары на низшие.

Следует иметь в виду, что заменяющий механизм имеет та­кой вид только для данного положения. Для каждого нового поло­жения длина звеньев и их взаимное расположение могут быть иными.

Определим степень подвижности исходного механизма

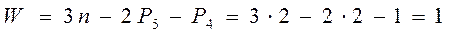
Степень подвижности заменяющего механизма

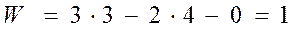
Сравнивая результаты, делаем вывод, что первое условие замены выполняется. Кроме того, если звено 1 повернуть на угол φ_1,то звено 2 повернется на соответствующий угол φ₂,т.е. второе условие также выполняется.

Сформулируем общие правила замены высших кинематических пар низшими:

1. Если высшие пары представляют собой соприкасающиеся окружности, то при замене низшие пары находятся в центре этих окружностей.

2. Если высшие пары представляют собой окружность или любую произвольную кривую, с одной стороны, и точечный контакт, с другой стороны, то кинематические пары замены находятся в точке контакта и в центре кривизны (рис. 1.5, а).

3. Если контакт в высшей паре происходит по линии, то замена осуществляется поступательной парой (рис. 1.5, б).

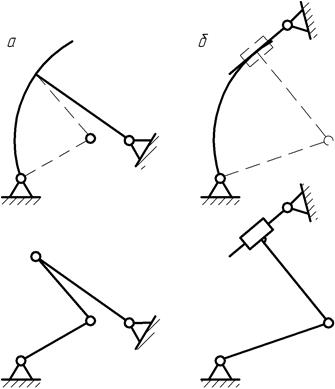
Рис. 1.5. Варианты замены высших кинематических пар низшими.

Последние два вывода представляют собой частные случаи:

- для точечного контакта радиус кривизны равен нулю (вращательная пара совпадает с точкой контакта);

- для прямой линии радиус кривизны равен бесконечности, т. е. в цепи замены движение должно осуществляться по прямой, а не по окружности (поступательная пара).