ЗАКОНЫ ПОДОБИЯ НАСОСОВ.

Моделирование насосов позволяет на основе подобия физических процессов в проточной части модельного насоса судить о гидродинамических характеристиках потока в натурном насосе. Практика показывает, что до изготовления машины в натуральную величину целесообразнее выполнить и испытать уменьшенную её модель, а потом, имея пересчетные формулы, вытекающие из условий подобия, получить рабочие параметры натурной машины.

Подобие насосов базируется на теории о механическом подобии движения реальной жидкости. Главное положение этой теории заключается в необходимости выполнения условий геометрического, кинематического и динамического подобия.

Геометрическое подобие предполагает равенство отношений сходственных размеров модели и натуры. Математически геометрическое подобие сравниваемых насосов определяется постоянством линейного коэффициента подобия (линейный масштаб)

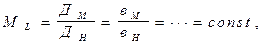(64)

где 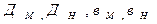– соответственно диаметры и ширина колёс модельного и натурного насосов.

Геометрическое подобие означает также подобие шероховатостей обтекаемых потоком поверхностей и зазоров между движущимися и неподвижными деталями насосов. Но выполнение этого требования в практике моделирования гидравлических машин возможно далеко не всегда. Действительно, при значениях M_L=20...30 какие-либо выступы или неровности размером 1...2 мм точно воспроизвести на модели не удается.

Кинематическое подобие предполагает равенство отношений скоростей в сходственных точках проточной части сравниваемых насосов или иначе говоря, полную идентичность полей безразмерных скоростей в модели и натуры. Применительно к насосам это означает подобие параллелограммов скоростей в соответствующих точках потока для всех элементов проточной части двух геометрически подобных, работающих в одинаковых режимах. Математически условия кинематического подобия могут быть выражены в виде ряда отношений:

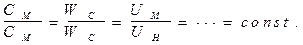(65)

Динамическое подобие выражается постоянством отношений сил одинаковой природы, действующих в сходственных точках геометрически и кинематически подобных машин. Так как этими силами являются силы давления, инерции, тяжести, трения, то подобие определяется равенством чисел Рейнольдса, Фруда, Струхаля, Эйлера.

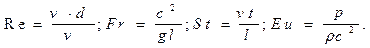(66)