Химическое равновесие
1. Во сколько раз увеличится скорость гомогенной реакции А + 2В = АВ2 при увеличении концентрации обоих исходных веществ в два раза?
Решение. В соответствии с основным законом химической кинетики скорость реакции до увеличения концентраций:
V1 = k * CA * CB²,
скорость реакции после увеличения концентраций:
V2 = k * 2CA * (2CB²) = 8k * CA* CB²
в результате увеличения обеих концентраций в два раза, скорость реакции возрастает в
V1 = 8k * CA* C²B = 8 раз.
V2 = k * CA * C²B
2.Во сколько раз следует увеличить концентрацию оксида углерода (II) в системе 2СО = СО2 + С, чтобы скорость реакции увеличилась в 4 раза?
Решение. Скорость реакции до увеличения концентрации
V1 = k * С²СО2,
скорость реакции после увеличения концентрации в неизвестное число (х) раз
V2 = k * (хсСО)² = x² * k * С²СО2.
В результате увеличения концентрации скорость возрастает в
V2 = k * c²СО = х²,
V1 x² * k * c²СО
А по условию задачи
V2 = x² = 4
V1
Отсюда 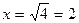
3. Во сколько раз увеличится скорость реакции
2С + О2 = 2СО
при увеличении парциального давления кислорода в 3 раза?
Решение. Углерод – твердое вещество, кислород – газ, реакция между ними является гетерогенной, и скорость ее зависит только от концентрации (парциального давления) кислорода:
V = k * pО2
При увеличении pО2 в 3 раза скорость реакции возрастает также в 3 раза, так как парциальное давление входит в уравнение основного закона химической кинетики для этой реакции в I степени.
На сколько градусов следует повысить температуру системы, чтобы скорость протекающей в ней реакции возросла в 30 раз, если температурный коэффициент γ = 2,5?
Решение. В соответствии с правилом Вант–Гоффа отношение скоростей реакции при двух температурах равно (см. уравнение 8.4):
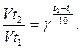
По условию задачи 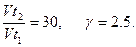
подставим числовые выражения в уравнение, описывающие правило Вант–Гоффа, получаем: 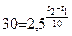
Логарифмируем полученное уравнение: 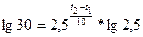
переносим числовые значения в правую часть уравнения, а неизвестную разность температур – в левую: 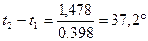
5. Вычислить температурный коэффициент реакции, если константа скорости ее при 120º составляет 5,88 * 10 ‾4 моль/м³*с, а при 170º - 6,70 * 10‾² моль/м³*с.
Решение. Величиной, отражающей зависимость скорости реакции от температуры в уравнении для основного закона химической кинетики (8.2), является константа скорости реакции. Таким образом, правило Вант–Гоффа справедливо и для отношения констант скоростей реакции при двух температурах:
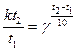
После подстановки числовых значений в это уравнение получаем:
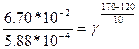
или 1,15 * 10².
После логарифмирования
2,061 = 5lgγ,
откуда
lgγ = 2,061 = 0,41.
С помощью таблицы антилогарифмов находим: γ = 2,52.
6. Вычислить равновесные концентрации водорода и иода, если известно, что их начальные концентрации равны и составляют по 0,02 моль/л, а равновесная концентрация равна 0,03 моль/л.
Решение. При решении задач на химическое равновесие приходится иметь дело с большим числом данных. Для их систематизации удобно воспользоваться таблицей, в вертикальных столбцах которой размещаются данные, относящиеся к каждому из реагирующих веществ, а в горизонтальных строках - три типа концентраций, о которых идет речь при решении задач: 1) исходные (начальные) концентрации веществ до начала реакций, 2) концентрации веществ, израсходованных в результате реакции, 3) равновесные концентрации, т.е. концентрации веществ в равновесной системе.
Для системы Н2 + J2 = 2HJ таблица с исходными данными имеет вид:
| Концентрации | Вещества | ||
| Н2 | J2 | HJ | |
| Исходные концентрации | 0,02 | 0,02 | |
| Израсходовано | - | - | - |
| Равновесные концентрации | ? | ? | 0,03 |
В условиях задачи дано, что равновесная концентрация HJ равна 0,03моль/л. Так как в начальный момент этого вещества в системе не было, то можно сделать вывод, что весь йодоводород, накопившийся в системе к моменту равновесия, образовался в результате взаимодействия исходных количеств водорода и йода. Из уравнения реакции видно, что для образования 2 молей йода нужно затратить 1 моль водорода и 1 моль йода; исходя из этого, можно составить пропорцию:
2 моль HJ образуется, если в реакцию вступает 1 моль Н2, 0,03 моль HJ образуется, если в реакцию вступает х моль Н2.
х = 0,03 * 1 = 0,015 моль/л.
Итак, для образования 0,03 моль/л HJ нужно израсходовать 0,015 моль/л водорода. Если концентрация водорода в системе до начала реакции составляла 0,02 моль/л и из них 0,015 моль/л вступило в реакцию, то равновесная концентрация водорода равна 0,02 – 0,015 = 0,05 моль/л. Аналогичный расчет можно сделать и для равновесной концентрации йода. Итоговая таблица имеет вид:
| Концентрации | Вещества | ||
| Н2 | J2 | HJ | |
| Исходные концентрации | 0,02 | 0,02 | |
| Израсходовано | 0,015 | 0,015 | - |
| Равновесные концентрации | 0,05 | 0,05 | 0,03 |
7. В системе СO + C12 = COC12 установить следующие равновесные концентрации: [C12] = 0,3 моль/л, [СО] = 0,2 моль/л, [COC12] = 1,2 моль/л. Вычислить константу равновесия систем и начальные (исходные) концентрации хлора и оксида углерода (II). Фосгена (COC12) в исходной смеси не было.
Решение. В соответствии с законом действия масс константа равновесия системы, состоящей из хлора, оксида углерода (II) и фосгена, может быть вычислена по уравнению
Kp = [COC12]
[СО] * [C12]
Подставляя в это уравнение численные выражения равновесных концентраций, получаем:
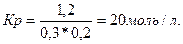
Для расчета исходных концентраций обратимся к уравнению реакции. Так как в этом уравнении все стехиометрические коэффициенты одинаковы и равняются единице, то можно сделать заключение, что при образовании 1 моля фосгена расходуется 1 моль оксида углерода (II) и 1 моль хлора. Следовательно, на образование 1,2 моля фосгена затрачено 1,2 моля оксида углерода (II) и 1,2 моля хлора. Эти рассуждения можно изобразить в виде пропорции:
для получения 1 M COC12 расходуется 1 М СО ( и 1 M C12)
для получения 1,2 М СО расходуется х М СО (и х М C12)
х = 1,2 М СО (или C12)
Исходные концентрации окиси углерода (II) и хлора можно вычислить, сложив равновесные концентрации и концентрации веществ, вступивших в реакции:
Cco = 0,2 + 1,2 = 1,4;
Сcl2=0,3+1,2=1,5.
Эту задачу удобно решать, используя таблицу, предложенную в предыдущем примере:
| Концентрация | Вещества | ||
| СО | С12 | СОС12 | |
| Исходные концентрации | 1,4 | 1,5 | - |
| Израсходовано | 1,2 | 1,2 | - |
| Равновесные концентрации | 0,2 | 0,3 | 1,2 |
8. Константа равновесия системы Н2 + J2 = 2HJ при некоторой температуре равна 40. Определить, сколько процентов водорода и йода превратится в йодоводород, если исходные концентрации водорода и йода одинаковы и составляют по 0,01 моль/ л, йодоводорода в исходной смеси не было.
Решение. В соответствии с уравнением реакции 1 моль водорода реагирует с одним молем йода. Следовательно, уменьшения концентраций этих веществ в результате их превращения в йодоводород равны. Обозначив эти уменьшения концентраций через х, равновесные концентрации обоих исходных веществ можно записать как 0,01 – х. Для установления соотношения между израсходованными количествами водорода и йода и концентрацией образовавшегося йодоводорода вновь обратимся к уравнению реакции.
Так как стехиометрические коэффициенты при химических формулах йода и водорода одинаковы и равны единице, а стехиометрический коэффициент при формуле йодоводорода равен двум можно сделать вывод, что в результате реакции между 1 молем водорода и 1 молем йода образуются 2 моля йодоводорода. Если же в реакцию вступают х молей водорода и х молей йода, то образуется 2х молей йодоводорода. Сводя все обозначения концентраций в таблицу, получаем:
| Концентрации | Вещества | ||
| Н2 | J2 | HJ | |
| Исходные концентрации | 0,01 | 0,01 | - |
| Израсходовано | х | х | - |
| Равновесные концентрации | 0,01 – х | 0,01 – х | 2х |
Подставляя обозначения равновесных концентраций и численную величину константы равновесия в уравнение закона действия масс для рассматриваемой системы, получаем:
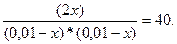
Решая это квадратное уравнение относительно х, находим два корня:
х1 = 0,0146 и
х2 = 0,0076. Первый корень не имеет смысла, так как противоречит закону сохранения вещества: х1 больше, чем исходные концентрации. Итак, в реакцию вступило по 0,0076 моль/л йода и водорода, что составляет в процентах от исходных концентраций по
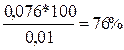
Приложение
Таблица 1
Плотность и процентное содержание раствора хлористого натрия
| Массовая доля, % | Плотность раствора, г/см3 | Массовая доля, % | Плотность раствора, г/см3 |
| 1,0053 | 1,1008 | ||
| 1,0125 | 1,1065 | ||
| 1,0196 | 1,1162 | ||
| 1,0268 | 1,1241 | ||
| 1,0340 | 1,1319 | ||
| 1,0413 | 1,1398 | ||
| 1,0486 | 1,398 | ||
| 1,0559 | 1,1478 | ||
| 1,0633 | 1,1639 | ||
| 1,0707 | 1,1722 | ||
| 1,0782 | 1,1804 | ||
| 1,0857 | 1,1888 | ||
| 1,0933 | 1,1972 |
Таблица 2
Дата добавления: 2016-09-06; просмотров: 4991;











