Влияние кривизны поверхности на равновесие фаз

До сих пор мы рассматривали поверхностные явления в системах, в которых сосуществующие фазы разделены плоской межфазной границей (с большим радиусом кривизны — см. ниже). Искривление поверхности раздела фаз вносит изменения в термодинамические свойства системы и обусловливает некоторые важные эффекты, относящиеся к числу капиллярных явлений.

Давления в контактирующих фазах, разделенных плоской поверхностью в условиях равновесия одинаковы. В отличие от этого давления в фазах, разделенных искривленной поверхностью, например, сферической, отличаются.

Пример. В этом легко убедиться на примере образования мыльных пузырей: если оставить в трубочке открытым отверстие, то под действием большего давления в пузырьке воздух начнет выходить, а размеры пузырька уменьшатся вплоть до его исчезновения. При этом уменьшаются поверхность пузырька и связанная с ней поверхностная энергия.

Что избыточное давление возрастает с уменьшением радиуса пузырька (радиуса кривизны — см. далее) можно доказать, выдув два пузырька разных размеров, а затем их соединив: маленький пузырек будет уменьшаться, а большой увеличиваться вплоть до полного перехода воздуха из малого в большой.

Вспомним, что из-за избыточной поверхностной энергии жидкая фаза благодаря своей подвижности приобретает сферическую форму в условиях невесомости. Вода в реках, морях, озёрах имеет плоскую поверхность только потому, что действует сила тяжести (F). С уменьшением количества жидкости её роль снижается, т.к. F ~ d³ (V), а S ~ d² ; S_уд=↑. Возрастающая роль поверхностной энергии проявляется в появлении кривизны поверхности жидкой фазы.

Рассмотрим изменение давления насыщенного пара жидкости при искривлении её поверхности (насыщенным называют пар, находящийся в равновесии со своей жидкостью) в трёх случаях: поверхность жидкости плоская, поверхность жидкости вогнутая и поверхность жидкости выпуклая (рис.2.29)

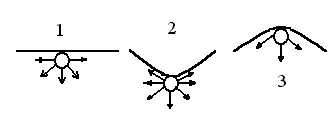
Рис.2.29. Межмолекулярные взаимодействия на искривлённой поверхности жидкости

Наиболее интенсивные взаимодействия в поверхностном слое жидкости наблюдаются в случае вогнутой поверхности (2). Здесь любая поверхностная молекула окружена максимальным числом «соседей». Выход её в газовую фазу в данном случае потребует наибольших затрат энергии. Поэтому следует ожидать, что над вогнутой поверхностью давление насыщенного пара будет минимальным.

В случае выпуклой поверхности жидкости (3) число молекул, окружающих выделенную поверхностную молекулу, минимально и, соответственно, давление насыщенного пара будет максимальным. Среднее положение занимает плоская поверхность.

Таким образом, давление насыщенного пара зависит от кривизны поверхности жидкости: над выпуклой поверхностью оно больше, а над вогнутой оно меньше, чем над плоской. И чем больше кривизна поверхности, тем сильнее отличаются друг от друга давления над плоской и искривленной поверхностью.

Рассмотрим результат влияния кривизны поверхности раздела между 2 несмешивающимися жидкостями на внутреннее давление Р в контактирующих фазах.

ΔР

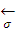r

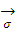
Рис. 2.30. Влияние кривизны поверхности раздела на внутреннее давление

Кривизна поверхности 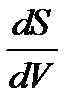вызывает изменение площади и положения межфазной поверхности, что можно выразить изменением поверхностной энергии (σ dS), изменяются объёмы фаз 1 и 2: dV₁= -dV_2, что ведет к изменению энергий ΔЕ фаз 1 и 2 на ΔЕ₁= р₁dV₁ и ΔЕ₂₌р₂dV₂ (р₁ и р₂ — внутренние давления внутри фаз).

Соотношение между поверхностной энергий и «объёмной» можно записать с помощью обобщенного уравнения 1 и 2-го законов термодинамики относительно энергии Гельмгольца F при Т=const:

dF=- р₁dV₁ - р₂dV₂ + σ dS (2.100)

При равновесии фаз ΔF=0, тогда

(р₁ - р₂) dV₂+ σ dS = 0, ΔР= р₂ - р₁= σ 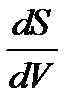(2.101)

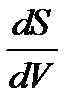— кривизна поверхности. Чем больше поверхностное натяжение, тем выше влияние кривизны поверхности. Вывод из уравнения следующий: