Формулы Ньютона-Котеса
Если подынтегральную функцию заменить каким-либо интерполяционным многочленом, то получим квадратурные формулы вида:
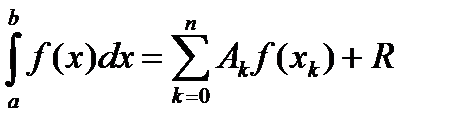
где хк – выбранные узлы интерполяции; Ak – коэффициенты, которые зависят от выбранных узлов, но не зависят от вида функции f(x); R – остаточный член, определяющий максимальную ошибку при использовании квадратурной формулы; k=0, 1, …, n.
Разбивая отрезок интегрирования [a, b] на n равных частей системой точек
xk = x0+kh; k=0, 1, …, n; x0=a; xn=b
и вычисляя подынтегральную функцию в полученных узлах
yk=f(x); k=0, 1, …, n,
получают квадратурные формулы для равноотстоящих узлов. Эти формулы называют формулами Ньютона-Котеса. Наиболее удобны при численном интегрировании интерполяционные многочлены невысоких порядков, при использовании которых получают достаточно простые составные формулы.
(1)Формула трапеций.
Формула трапеций получается в случае использования интерполяционного многочлена 1-го порядка:
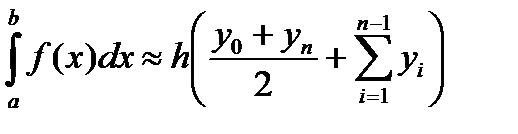
Остаточный член имеет вид:
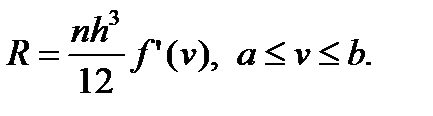
Использование формулы трапеций при вычислении определенного интеграла приводит к ошибке
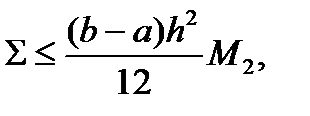 где
где ![]()
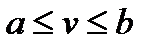
Для нахождения приближенного значения определенного интеграла по формуле трапеций можно использовать алгоритм, схема которого представлена на рис. 5.5.
Ошибка ограничения для метода трапеций больше, нежели чем для других формул Ньютона-Котеса, но его привлекательность заключается в простой реализации. Кроме того, незначительное усложнение алгоритма позволяет существенно снизить погрешность вычислений, поэтому формула трапеций достаточно часто используется (в сочетании с другими формулами).
Например, в случае аппроксимации подынтегральной функции интерполяционным многочленом Эрмита получают формулу Эйлера:
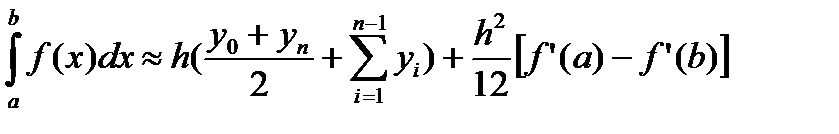
Остаточный член этой формулы свидетельствует о том, что небольшая добавка к формуле трапеций существенно повышает ее точность.
В последней формуле значения производных можно заменить двусторонними разностями
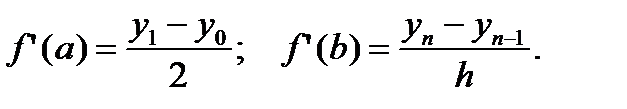
В результате формула Эйлера превращается в формулу Грегори, но общий порядок точности понизится с четвертого до третьего.
(2) Формула парабол (Симпсона)
Используя интерполяционный многочлен 2-го порядка (параболу) получают формулу численного интегрирования – формулу Симпсона:
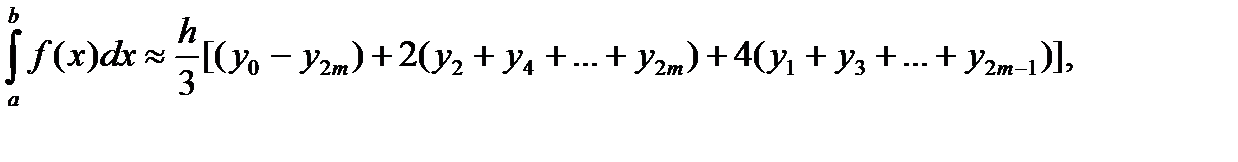
где 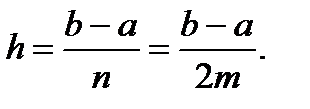
| Начало |
| Ввод a, b, n |
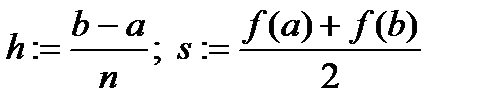 |
| x:=a+h |
| s:=s+f(x) x:=x+h |
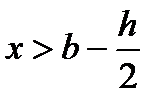 |
| s:=sּh |
| Вывод s |
| Конец |
| Нет |
| Да |
| Рис. 5.5 Алгоритм вычисления определенного интеграла по формуле трапеций |
На рис. 5.6 показана схема алгоритма, реализующего вычисления по формуле парабол. При реализации формулы число узлов обязательно нечетно, т. е. число участков разбиения интервала интегрирования должно быть четным: n=2m. В алгоритме использован прием, при котором число повторений цикла уменьшается в два раза, т. е. дважды реализуется модификация параметра цикла, что уменьшает время выполнения алгоритма. Метод Симпсона считается одним из наиболее применяемых методов численного интегрирования, обеспечивающим достаточно хорошую точность вычислений.
| Начало |
| Ввод a, b, n |
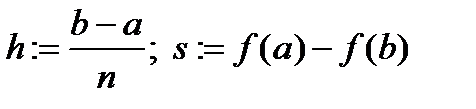 |
| x:=a+h |
| s:=s+4f(x) x:=x+h s:=s+2f(x) x:=x+h |
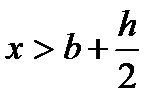 |
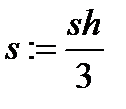 |
| Вывод s |
| Конец |
| Нет |
| Да |
| Рис. 5.6 Алгоритм вычисления определенного интеграла по формуле Симпсона |
(3)Формула Ньютона (правило трех восьмых)
Более высокую точность вычисления обеспечивает интерполирование подынтегральной функции полиномом третьей степени. В результате получают формулу Ньютона (правило трех восьмых):
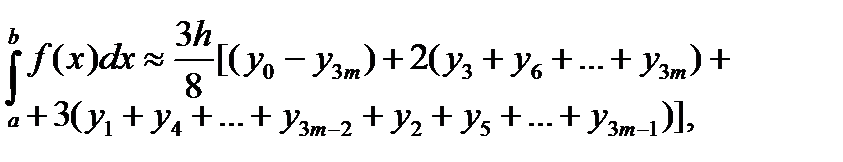
где 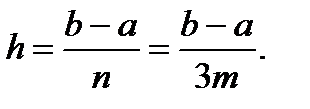 Схема алгоритма численного интегрирования по правилу трех восьмых показана на рис. 5.7 Практическое применение нашли также четвертая, пятая и шестая формулы Ньютона-Котеса, однако их использование приводит к более громоздким схемам.
Схема алгоритма численного интегрирования по правилу трех восьмых показана на рис. 5.7 Практическое применение нашли также четвертая, пятая и шестая формулы Ньютона-Котеса, однако их использование приводит к более громоздким схемам.
| Рис. 5.7 Алгоритм вычисления определенного интеграла по формуле Ньютона |
| Начало |
| Ввод a, b, n |
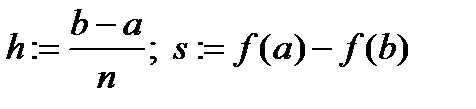 |
| x:=a+h |
| s:=s+4f(x) x:=x+h s:=s+2f(x) x:=x+h s:=s+2f(x) x:=x+h |
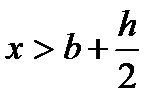 |
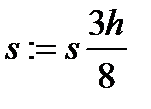 |
| Вывод s |
| Конец |
| Нет |
| Да |
Рассмотренные выше циклические структуры характеризуются одной общей особенностью – во всех рассмотренных примерах заранее можно определить число повторений тела цикла. Задачи, где число повторений заранее неопределенно, приводят к так называемым циклам с неизвестным (до начала цикла) числом повторений.
Пусть, например, надо определить интервал (a, b), внутри которого функция y=f(x)пересекает ось абсцисс (внутри этого интервала функция f(x) обращается в ноль, т. е. f(x)=0). На рис. 5.8 показано возможное решение поставленной задачи в форме соответствующего графика. Первоначально можно предположить, что искомый интервал может иметь границы a=x0 и b=x0+hx. Если в указанном интервале нет искомой точки, то искать ее следует в следующем интервале (a+hx , b+hx). Последовательный анализ интервалов продолжается до тех пор, пока не будет достигнут искомый результат. Необходимое условие того, что функция y=f(x) пересекает ось абсцисс, может быть записано в следующем виде: ya·yb<0, где ya = f(a); yb = f(b).
На рис. 5.9 приведена схема алгоритма нахождения интервала (a, b), с использованием оператора цикла с предусловием.
y0
y1
y2
y
a
b
x0
x1
x2
xn
x
hx
Рис. 5.8 Нахождение интервала, внутри которого функция пересекает ось абсцисс
Условие продолжения цикла определено с помощью логической переменной v. Значение переменной v формируется из двух условий. С одной стороны выход из цикла возможен в тех случаях, когда найден искомый интервал (a, b), т. е. выполняется условие f(a)f(b)<0. С другой стороны, точка пересечения с осью абсцисс может отсутствовать, тогда выход из цикла осуществляется в результате достижения граничной (конечной) точки xn. Объединенное условие продолжения цикла
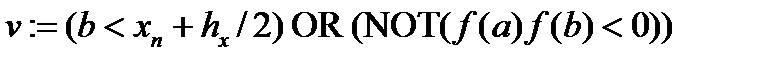
Начало
Ввод x0, hx, xn
a:=x0; b:=x0+hx ya:=f(a); yb:=f(b)
v
a:=a+hx; b:=b+hx ya:=f(a); yb:=f(b)
b>xn+hx/2
Точки пересечения нет
Вывод a, b
Конец
Нет
Да
Да
Нет
Рис. 5.9 Схема алгоритма определения интервала, внутри которого функция пересекает ось абсцисс
Дата добавления: 2016-05-31; просмотров: 6421;











