Метод половинного деления

Метод половинного деления является более универсальным, всегда приводит к искомому результату, хотя и требует большого объема вычислений. Для нахождения корня уравнения f(x)=0, принадлежащего отрезку [a, b], делим отрезок пополам z = (a+b)/2 (см. рис. 5.12,а). Далее рассмотрим значения функции y = f(x) в точках x = a и x = z. Если значения f(a)и f(z)разных знаков, т. е. f(a) f(z) < 0, то исходный отрезок[a, b] уменьшим в два раза путем переноса точки x = b в точку x = z. Новый отрезок [a, b] вновь делим пополам (см. рис. 5.12,б) и так как f(a) f(z) < 0, то переносим точку x = a в точку x = z, уменьшая [a, b] в два раза. Повторяем указанную процедуру до тех пор, пока длина отрезка, содержащего корень, не станет меньше заданной погрешности ε. Любое значение 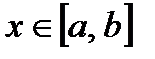является искомым значением корня, однако на практике в качестве корня выбирают середину отрезка, т. е. x = (a+b)/2.

При организации итерационного цикла вычисляется последовательность отрезков

[a₀, b₀], [a₁, b₁], …, [a_n, b_n], … ,

для которой

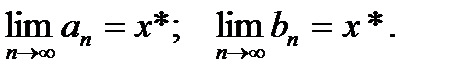
Для контроля точности вычисления корня можно использовать следующую последовательность значений

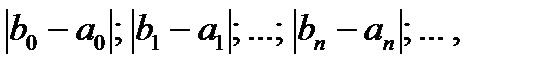
поэтому условие выхода из цикла

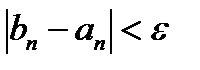
или условие продолжения цикла

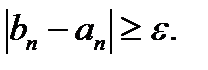
Схема алгоритма уточнения корня алгебраического уравнения методом половинного деления приведена на рис. 5.13. В результате выполнения такого алгоритма выводится значение корня (с заданной погрешностью), а также значение функции f(x), которое очень близко к нулевому значению и может быть использовано для контроля правильности полученного результата.

y=f(x)

y

F(z)

0 a

x^* z b

f(a)

a)

y

y=f(x)

0 a x^*

f(z) z b x

f(a)

b)

Рис. 5.12 Графическая иллюстрация метода половинного деления

Начало

Ввод a, b,ε

|b-a| ≥ ε

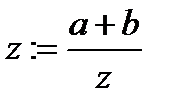
f(z)f(a) < 0

a:=z

b:=z

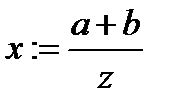
Вывод x, f(x)

Конец

Нет

Да

Да

Нет

Рис. 5.13 Схема алгоритма уточнения корня методом половинного деления

Метод касательных

Для обеспечения сходимости метода касательных (метода Ньютона) необходимо, чтобы производные f'(x)и f"(x)были определены, непрерывны и сохраняли постоянные знаки на отрезке [a, b]. На рис. 5.14 представлена геометрическая интерпретация метода Ньютона.

Выберем некоторую точку x₀ на отрезке [a, b] и проведем касательную к кривой y=f(x) в точке P₀(x₀, y₀). Ее уравнение

y = y₀ + f'(x₀)(x–x₀),

где y₀ = f(x₀).

Новое приближение корня х₁, равно абсциссе точки пересечения касательной с осью абсцисс, т. е.

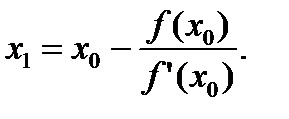
Рис. 5.14 Геометрическая интерпретация метода касательных

0 a x* x2 x1 x0 b x

y=f(x)

y

y₀

y₁

y₂

Выберем некоторую точку x₀ на отрезке [a, b] и проведем касательную к кривой y=f(x) в точке P₀(x₀, y₀). Ее уравнение

y = y₀ + f'(x₀)(x–x₀),

где y₀ = f(x₀).

Новое приближение корня х₁, равно абсциссе точки пересечения касательной с осью абсцисс, т. е.

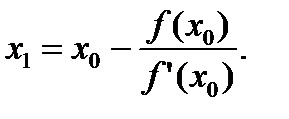
Проведя касательную через точку P₁(x₁, y₁), получим второе приближение корня x₂. Вычисление приближений корня по формуле

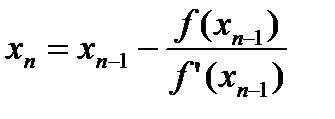
продолжается до выполнения неравенства

,

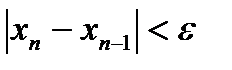где ε – абсолютная погрешность определения корня уравнения.

Начальное приближение х₀ выбирают таким образом, чтобы выполнялось условие

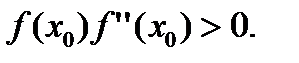
В противном случае сходимость метода Ньютона не гарантируется. На практике выбирают x₀ = a или x₀ = b, в зависимости от того, в какой из этих точек выполняется указанное условие. Схема алгоритма уточнения корня методом Ньютона (методом касательных) приведена на рис. 5.15.

Начало

Ввод a, b,ε

f(a)f"(a) > 0

f(b)f"(b) > 0

x:=a

x:=b

"ошибка"

Останов

h:=f(x)/f'(x) x:=x-h

|h| < ε

Вывод x, f(x)

Конец

Нет

Да

Нет

Да

5.15 Схема алгоритма уточнения корня методом касательных

Метод хорд

Геометрическая интерпретация метода хорд приведена на рис. 5.16. Проведем через точки (a, y_a) и (b, y_b) прямую. Уравнение этой прямой:

>

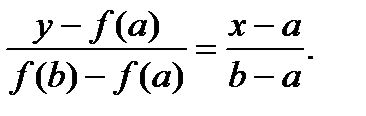
0 a x0 x1 x2 b x

yb=f(a)

y

y=f(x)

yb=f(b)

Рис. 5.16 Графическая иллюстрация метода хорд

Начальное приближение корня равно абсциссе точки пересечения и оси абсцисс (легко определяется также из соответствующих пропорций):

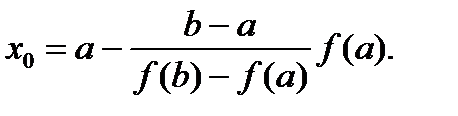
Из двух отрезков [a, x₀] и [x₀, b] выберем тот, на концах которого функция f(x) имеет разные знаки (т. е. отрезок, содержащий корень уравнения). Проведем секущую на новом отрезке [x₀, b] и получим следующее приближение корня x₁. Формируем последовательность x₀, x₁, x₂, …, x_n, … до выполнения условия

|x_n – x_n-1| < ε.

Схема алгоритма уточнения корня методом хорд (методом пропорциональных частей) приведена на рис. 5.17.

Начало

Ввод a, b, ε

z:=f(a); t:=f(b) x:=a

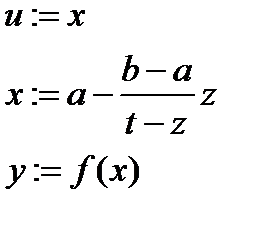
y·z < 0

A:=x; z:=y

b:=x; t:=y

|n-z| < ε

Вывод x, f(x)

Конец

Нет

Нет

Да

Да

Рис. 5.17 Схема алгоритма уточнения корня методом хорд