Уравнения, допускающие понижение порядка.
Рассмотрим типы дифференциальных уравнений 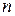 -го порядка, для которых можно понизить порядок уравнений.
-го порядка, для которых можно понизить порядок уравнений.
1) Уравнение вида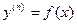 .
.
Общее решение данного уравнения можно получить путем 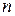 последовательных интегрирований, а именно
последовательных интегрирований, а именно
 ;
;
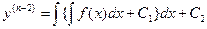 и т.д.
и т.д.
Пример 1. Решить уравнение
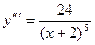 ,
, 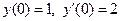 ,
, 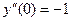 .
.
Решение.
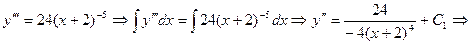
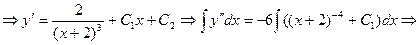
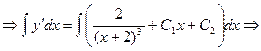
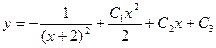 .
.
Подставив последовательно в полученные равенства начальные условия, определим 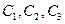 :
:
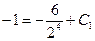 ;
; 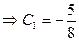
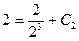 ;
; 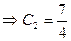
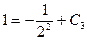 ;
; 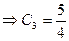 .
.
Частным решением данного уравнения будет
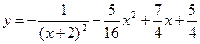 .
.
2)Уравнение вида .
.
Данное дифференциальное уравнение 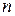 -го порядка не содержит неизвестной функции
-го порядка не содержит неизвестной функции 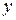 и ее производных до
и ее производных до 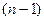 -го порядка. Вводим новую функцию
-го порядка. Вводим новую функцию 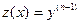 и, следовательно,
и, следовательно, 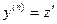 . Получим дифференциальное уравнения первого порядка
. Получим дифференциальное уравнения первого порядка  , где неизвестной функцией является функция
, где неизвестной функцией является функция 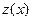 . В частном случае, когда
. В частном случае, когда 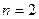 , дифференциальное уравнение второго порядка
, дифференциальное уравнение второго порядка  , не содержащее неизвестной функции
, не содержащее неизвестной функции 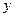 , подстановкой
, подстановкой 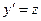 приводится к уравнению первого порядка
приводится к уравнению первого порядка  .
.
Пример 2. Проинтегрировать дифференциальное уравнение
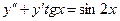 .
.
Решение. Это уравнение не содержит 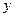 . Полагаем
. Полагаем 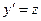 ,
, 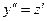 , получим линейное дифференциальное уравнение первого порядка
, получим линейное дифференциальное уравнение первого порядка
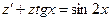 .
.
Здесь 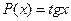 ,
,  . Найдем общее решение уравнения:
. Найдем общее решение уравнения:
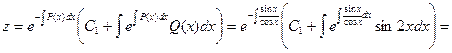
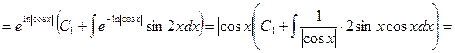
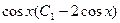 .
.
Итак,
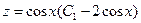
или
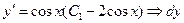
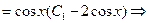
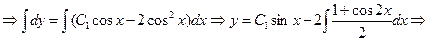
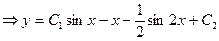 .
.
Получили общее решение данного дифференциального уравнения.
Пример 3. Решить уравнение 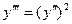 .
.
Решение. Полагаем 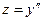 ,
, 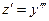 . Тогда данное уравнение примет вид:
. Тогда данное уравнение примет вид:
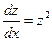 .
.
Разделим переменные
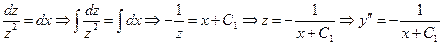 .
.
В результате последовательного интегрирования получим
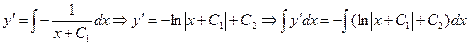 ;
;
К интегралу справа применим формулу интегрирования по частям, полагая
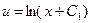 ,
, 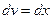 ,
,  ,
, 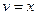 .
.
Тогда
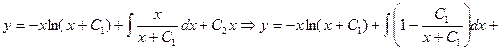
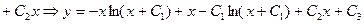 .
.
Итак, 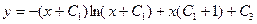 .
.
3)Уравнение вида .
.
Данное уравнение не содержит независимую переменную 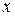 . Полагаем
. Полагаем 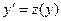 , тогда
, тогда
 .
.
Рассматриваемое уравнение примет вид:
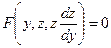 ,
,
где неизвестной функцией является 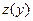 , а независимой переменной
, а независимой переменной 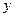 .
.
Пример 4. Проинтегрировать дифференциальное уравнение
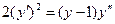 .
.
Решение. Полагая 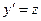 ,
,  , получим дифференциальное уравнение первого порядка
, получим дифференциальное уравнение первого порядка
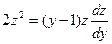 или
или  .
.
Приравняем первый множитель нулю:
 или
или 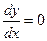 , т.е.
, т.е. 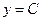 .
.
Функция 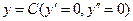 обращает данное уравнение в тождество, следовательно, является решением. Общее решение данного дифференциального уравнения получим, проинтегрировав уравнение
обращает данное уравнение в тождество, следовательно, является решением. Общее решение данного дифференциального уравнения получим, проинтегрировав уравнение
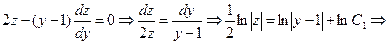
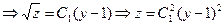 .
.
Производя обратную замену 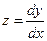 , получим
, получим
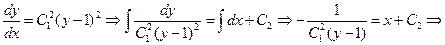
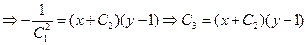 , где
, где 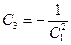 .
.
Пример 5. Найти частное решение уравнения
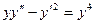 при условии
при условии 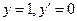 при
при 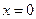 .
.
Решение. Полагаем 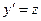 ,
,  и уравнение преобразуется в следующее:
и уравнение преобразуется в следующее:
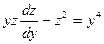 или
или 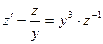 .
.
Получили уравнение Бернулли. Преобразуем уравнение:  . Полагаем
. Полагаем 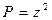 , тогда
, тогда 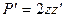 . Рассматриваемое уравнение примет вид:
. Рассматриваемое уравнение примет вид:
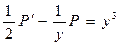 или
или  .
.
Получили линейное дифференциальное уравнение первого порядка. Его общее решение имеет вид:
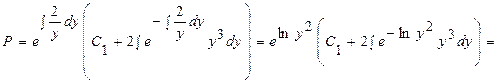
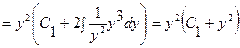 , т.е.
, т.е.  .
.
Произведя обратную замену  , получим
, получим
 или
или 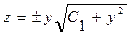 . Из условия
. Из условия  при
при 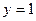 имеем
имеем 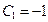 . Следовательно,
. Следовательно, 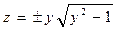 или
или 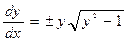 . Интегрируя, имеем:
. Интегрируя, имеем:
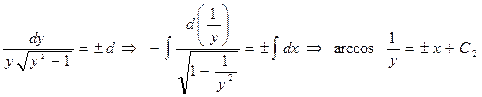 .
.
Полагая 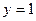 и
и 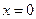 , получим
, получим 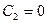 , откуда
, откуда 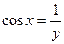 или
или 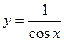 .
.
Пример 6. Если тело медленно погружается в воду, то его скорость  и ускорение
и ускорение 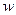 приближенно связаны уравнением
приближенно связаны уравнением 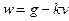 ,
,
где  и
и 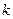 - постоянные. Установить зависимость между пройденным путем
- постоянные. Установить зависимость между пройденным путем 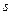 и временем
и временем 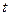 , если при
, если при 
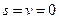 .
.
Решение.Так как ускорение 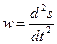 и скорость
и скорость 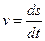 , то зависимость между
, то зависимость между 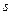 и
и 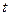 выражается дифференциальным уравнением второго порядка
выражается дифференциальным уравнением второго порядка
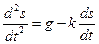 ,
,
не содержащим неизвестной функции 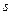 . Положив
. Положив 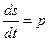 ,
,  , получим
, получим 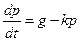 , или
, или 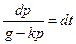 .
.
Проинтегрируем обе части равенства: 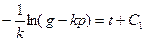 . Определим
. Определим 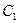 , учтя, что
, учтя, что 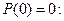
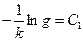 .
.
Подставим найденное значение 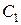 в предыдущее равенство:
в предыдущее равенство:
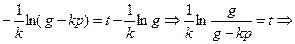
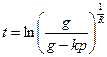 , или
, или 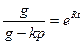 .
.
Откуда
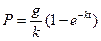 , или
, или 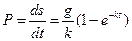
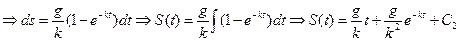 .
.
Из начального условия 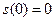 определим
определим 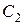 :
:
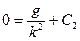 ;
; 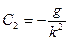 .
.
Подставив найденное значение 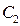 в предыдущее равенство, получим искомую зависимость
в предыдущее равенство, получим искомую зависимость
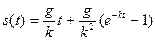 .
.
Дата добавления: 2016-07-27; просмотров: 2688;











