Дифференциальные уравнения высших порядков. Задачи Коши для дифференциальных уравнений высших порядков.
Дифференциальные уравнения порядка выше первого называются ДУ высших порядков, которое в общем виде записывается
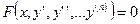 .
.
Общее решение ДУ n-го порядка является функцией вида
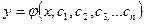
содержащей n произвольных, не зависящих от х постоянных.
Решение ДУ, получающееся из общего решения при конкретных значениях постоянных 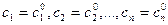 называется частным решением.
называется частным решением.
Задача нахождения решения ДУ высшего порядка сложнее, чем первого. Поэтому рассмотрим лишь отдельные виды ДУ высших порядков.
Определение. ДУ второго порядка называется уравнение вида
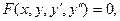 (1.1)
(1.1)
где 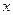 - независимая переменная,
- независимая переменная, 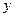 - искомая функция,
- искомая функция, 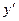 и
и 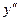 - соответственно первая и вторая производные.
- соответственно первая и вторая производные.
В случае, когда из уравнения можно выразить 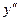 , оно примет вид
, оно примет вид
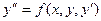 . (1.2)
. (1.2)
Это уравнение называется уравнением второго порядка,разрешенным относительно производной.
Пример. Колебания материальной точки массы  , находящейся под действием упругой силы, величина которой пропорциональна отклонению
, находящейся под действием упругой силы, величина которой пропорциональна отклонению 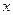 точки от положения равновесия, при наличии периодической силы, численно равной
точки от положения равновесия, при наличии периодической силы, численно равной 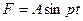 , описывается уравнением движения точки
, описывается уравнением движения точки
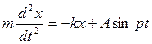 ,
,
где 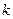 - коэффициент пропорциональности (
- коэффициент пропорциональности ( 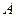 и
и 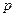 - постоянные, сопротивление среды отсутствует.)
- постоянные, сопротивление среды отсутствует.)
Обычно оно записывается в виде
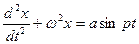 ,
,
где 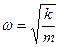 и
и 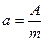 . Здесь
. Здесь 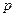 - частота внешней силы,
- частота внешней силы, 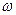 - частота свободных колебаний.
- частота свободных колебаний.
Это пример ДУ второго порядка; называется оно уравненим вынужденных колебаний материальной точки.
Как и в случае уравнения первого порядка, решением дифференциального уравнения теперь уже второго порядка называется функция 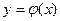 , определенная на некотором интервале
, определенная на некотором интервале 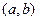 , которая при подстановке в дифференциальное уравнение обращает его в тождество. График решения называется интегральной кривой.Имеет место теорема существования и единственности решения уравнения второго порядка.
, которая при подстановке в дифференциальное уравнение обращает его в тождество. График решения называется интегральной кривой.Имеет место теорема существования и единственности решения уравнения второго порядка.
Теорема (о существовании и единственности решения дифференциального уравнения первого порядка). Если в уравнении 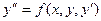 функция
функция 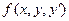 и ее частые производные
и ее частые производные 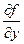 ,
, 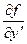 непрерывны в некоторой области
непрерывны в некоторой области 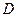 пространства переменных
пространства переменных 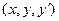 , содержащей точку
, содержащей точку 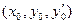 , то в некоторой окрестности точки
, то в некоторой окрестности точки 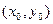 существует единственное решение этого уравнения
существует единственное решение этого уравнения 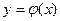 , удовлетворяющее условию
, удовлетворяющее условию 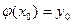 ,
, 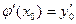 .
.
Геометрический смысл теоремы заключается в том, что существует и притом единственная функция 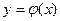 , график которой проходит через точку
, график которой проходит через точку 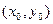 , с заданным угловым коэффициентом
, с заданным угловым коэффициентом 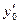 касательной.
касательной.
Условия, что функция 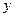 должна равняться заданному числу
должна равняться заданному числу 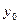 , а
, а 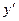 должно равняться числу
должно равняться числу 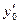 при
при 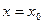 , называется начальными условиями (н.у.). Они записываются в виде
, называется начальными условиями (н.у.). Они записываются в виде 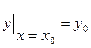 ,
, 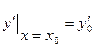 или
или 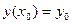 ,
, 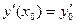 .
.
Задача отыскания решений уравнения, удовлетворяющего начальным условиям, носит название задачи Коши.
Пример. Найти решение уравнения 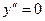 , удовлетворяющее н. у.
, удовлетворяющее н. у.
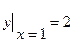 ,
, 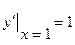
Определение. Общим решением ДУ второго порядка называется функция 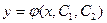 , содержащая две произвольные постоянные и 1) удовлетворяющая этому уравнению при любых постоянных
, содержащая две произвольные постоянные и 1) удовлетворяющая этому уравнению при любых постоянных 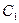 и
и 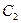 , и 2) которые могут быть определены единственным образом при заданных н.у.
, и 2) которые могут быть определены единственным образом при заданных н.у.
Определение. Частным решением ДУ второго порядка в области 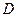 называется функция
называется функция 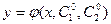 , полученная из общего решения при определенных значениях постоянных
, полученная из общего решения при определенных значениях постоянных 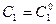 и
и 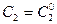 .
.
Пример. Общее решение уравнения 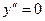 есть функция
есть функция 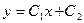 - это семейство прямых. Оно получается двукратным интегрированием данного уравнения. Найти частное решение, удовлетворяющее н.у.
- это семейство прямых. Оно получается двукратным интегрированием данного уравнения. Найти частное решение, удовлетворяющее н.у. 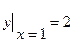 ,
, 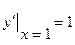 означает найти решение, проходящее через точку
означает найти решение, проходящее через точку 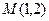 , с угловым коэффициентом равным 1. Подставим н.у. в общее решение и получим систему уравнений относительно
, с угловым коэффициентом равным 1. Подставим н.у. в общее решение и получим систему уравнений относительно 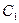 и
и 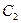 :
:
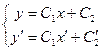
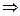
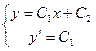
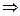
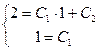
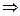
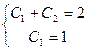
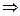
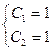 .
.
Таким образом, искомое частное решение – это прямая 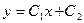
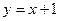 .
.
Дата добавления: 2016-07-27; просмотров: 2756;











