Простейшие типы дифференциальных уравнений первого порядка.

Замечание: При нахождении решения линейного уравнения (9) можно пользоваться формулой (14).

Уравнение вида

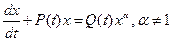(15)
называется уравнением Бернулли.

Прежде всего отметим, что при 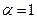уравнение (15) принимает вид

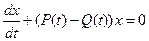
то есть является уравнением с разделяющимися переменными, общее решение которого

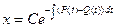
Разумеется, считаем, что 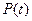и 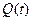непрерывны на некотором интервале .

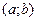Область изменения величины 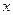в (15) определяется значением 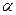, то есть областью существования функции .

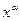Для решения д.у. (15) делаем замену

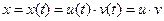, (16)
то есть вместо одной неизвестной функции вводим две! Но появляется возможность при этом выбрать одну функци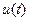й или 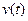, как будет удобнее. Постановка (16) в (15) дает

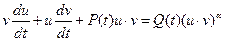. (17)
Найдем 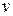из уравнения

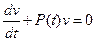(18)
то есть положим

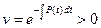. (19)
При этом среди первообразных для 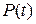выберем наиболее удобную. С учетом (18) уравнение (17) принимает вид

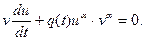
Это уравнение с разделяющимися переменными 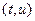и общее решение

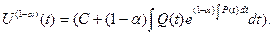(20)
его с учетом (19) имеет вид

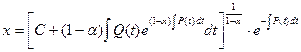(21)
По (16) окончательно

Разумеется, не следует запоминать формулу (21). Надо использовать алгоритм, описанный в (16) – (19).

Рассмотрим дифференциальное уравнение

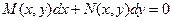. (22)
Предположим, что 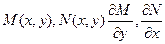, дифференцируемые в некоторой области .

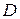Определение. Если левая часть уравнения (22) представляет собой полный дифференциал некоторой функции 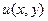, то (22) называется уравнением в полных дифференциалах.