Структура общего решения ЛНДУ.
Пусть дано неоднородное ЛДУ 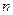 -го порядка
-го порядка
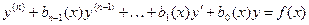 ,
, 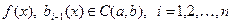 .
.
Определение. Уравнение 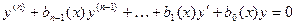 , левая часть которого совпадает с левой частью данного уравнения, называется соответствующим ему однородным уравнением.
, левая часть которого совпадает с левой частью данного уравнения, называется соответствующим ему однородным уравнением.
Структура общего решения (ОР) ЛНДУ дается следующей теоремой.
Теорема. Общимрешением ЛНДУ является сумма его произвольного частного решения и общего решения соответствующего ЛОДУ: 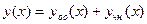 .
.
Теорема означает, что для того, чтобы получить общее решение ЛНДУ надо решить соответствующее ЛОДУ, т.е. найти его ОР, затем, найти какое-нибудь частное решение ЛНДУ и их сложить.
Рассмотрим теперь методы нахождения частного решения неоднородного ЛДУ.
Метод Лагранжа (метод вариации произвольных постоянных)
Пусть дано неоднородное ЛДУ 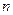 -го порядка
-го порядка
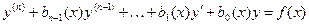 , (1) (3.20)
, (1) (3.20)
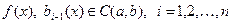 .
.
Предположим, что найдена или известна фундаментальная система решений соответствующего однородного уравнения
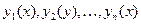 . (2) (3.21)
. (2) (3.21)
Решение уравнения (1) (3.20) будем искать в виде
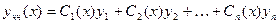 , (3) (3.22)
, (3) (3.22)
т.е. предполагая 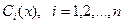 не постоянными, а переменными и дифференцируемыми на
не постоянными, а переменными и дифференцируемыми на 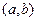 величинами. Эти функции пока неизвестные произвольные, для нахождения их нужно иметь
величинами. Эти функции пока неизвестные произвольные, для нахождения их нужно иметь 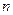 условий. Продифференцируем
условий. Продифференцируем 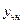
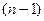 - раз
- раз
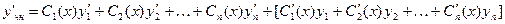 ,
,
каждый раз, что сумма в квадратных скобках равна нулю.
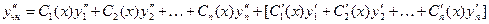 .
.
И т.д., найдем 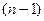 производную
производную
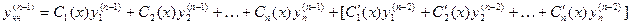 Полагая выражение в квадратных скобках равным нулю, продифференцируем еще раз
Полагая выражение в квадратных скобках равным нулю, продифференцируем еще раз
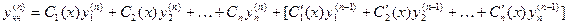 .
.
Подберем 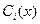 так, чтобы функция (3) (3.22) являясь решением уравнения (1) (3.20). Подставляя функцию (3) (3.22) и ее производные левую часть линейного дифференциального уравнения (1) (3.20), получим
так, чтобы функция (3) (3.22) являясь решением уравнения (1) (3.20). Подставляя функцию (3) (3.22) и ее производные левую часть линейного дифференциального уравнения (1) (3.20), получим
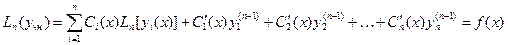 .
.
Так как 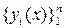 - ФСР однородного ЛДУ, то получим последнее
- ФСР однородного ЛДУ, то получим последнее 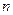 - ое условие относительно
- ое условие относительно 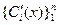 .
.
Таким образом, для нахождения неизвестных функций 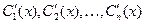 получили систему линейных алгебраических уравнений
получили систему линейных алгебраических уравнений
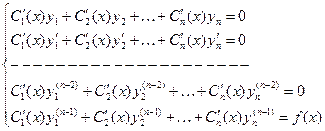 (4) (3.23)
(4) (3.23)
Решая ее методом Крамера (что можно сделать, т.к. главный определитель системы равен вронскиану 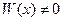 , ибо
, ибо 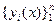 - ФСР), имеем
- ФСР), имеем
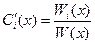 ,
, 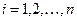 ,
,
где определители 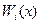 получаются из главного
получаются из главного 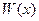 заменой элементов
заменой элементов 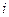 -го столбца свободными членами системы.
-го столбца свободными членами системы.
Пример. Найдем общее решение неоднородного ЛДУ второго порядка 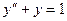 .
.
Найдем вначале ФСР однородного уравнения 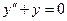 .
.
Из характеристического уравнения 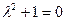 получим
получим
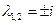 , т.е.
, т.е. 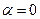 ,
, 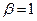 , поэтому
, поэтому 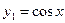 ,
, 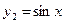 .
.
Подставив эти функции в (4) (3.23) получим
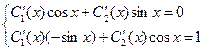

Отсюда
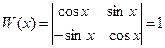 ,
, 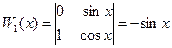 ,
, 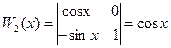 .
.
Следовательно 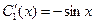 ,
, 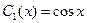 ,
, 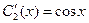 ,
, 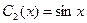 ,
, 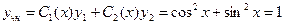 . Окончательно получим общее решение исходного уравнения
. Окончательно получим общее решение исходного уравнения
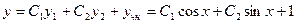 .
.
Дата добавления: 2016-07-27; просмотров: 4367;











