ЛНДУ с постоянными коэффициентами.

Метод вариации можно использовать для любых линейных дифференциальных уравнений с любой непрерывной правой частью. А метод неопределенных коэффициентов можно применять только для уравнений с постоянными коэффициентами и только с правой частью определенных видов. Преимущество этого метода в том, что можно находить частное решение неоднородного уравнения, не прибегая к операции интегрирования.

Рассмотрим неоднородное ЛДУ 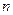-го порядка с постоянными коэффициентами

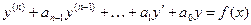. (5) (3.24)

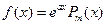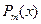1) Пусть первая часть , где - многочлен степени .

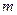а) Если 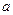(коэффициент в показателе экспоненты) не является корнем характеристического уравнения, тогда частное решение неоднородного уравнения ищется в той же форме, т.е.

,

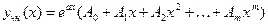где 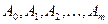- не определены. Для их нахождения нужно продифференцировать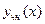 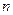раз и подставить его в уравнение (5) (3.24). А дальше коэффициенты находятся аналогично способу неопределенных коэффициентов при интегрировании, т.е. приравниваются коэффициенты при одинаковых степенях .

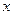Пример: Найти частное решение уравнения

.

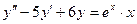Составляем характеристическое уравнение 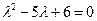, корни его 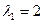, 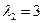. Значит, 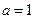не является корнем характеристического уравнения.

Будем искать частное решение в виде .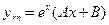

Найдем первую и вторую производные

,

.

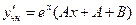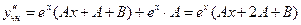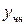Подставим в уравнение:

.

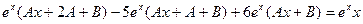
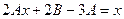Отсюда, приравнивая коэффициенты при одинаковых степенях справа и слева, получим

,

;

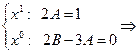
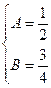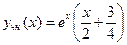б) Пусть 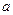является корнем характеристического уравнения кратности 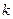. Тогда частное решение ищется в той же форме, но с сомножителем 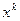, т.е.

.

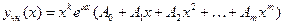И далее аналогично пункту а).

Пример. .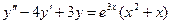

Характеристическое уравнение 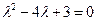имеет корни его 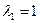, 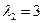. Значит, 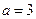является корнем характеристического уравнения кратности один. Поэтому частное решение надо искать в виде

.

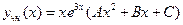Пример: .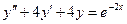

Характеристическое уравнение 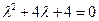имеет корни корень 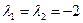кратности два, т.е. 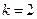. Поэтому решение ищем в виде

.

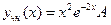Продифференцируем его дважды:

,

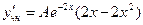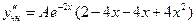
и подставим в уравнение. Вынося 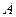и экспоненту, получим

,

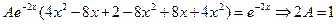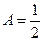
Частным решением является функция

.

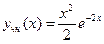2) Пусть правая часть уравнения (5) (3.24) есть

.

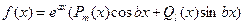а) Если комплексное число 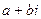не является корнем характеристического уравнения, тогда частное решение неоднородного уравнения ищется в виде

,

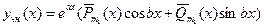где 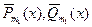- многочлены степени 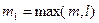с неопределенными коэффициентами.

Пример: .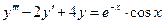

Характеристическое уравнение 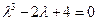можно представить виде 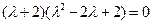, т.е. 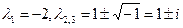, значит 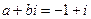не является корнем характеристического уравнения. Решение будем искать в виде .

,

,

.

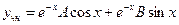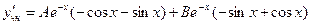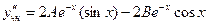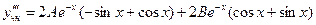Подставляя эти производные в уравнение, после сокращения получим

.

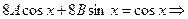
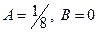Следовательно, частным решением является функция .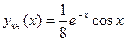

б) Если 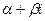является корнем характеристического уравнения кратности 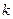, тогда частное решение неоднородного ЛДУ (5)(3.26) ищется в виде

, .

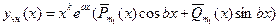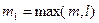Пример: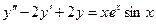

Характеристическое уравнение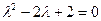

имеет корни 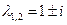, следовательно, 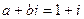является корнем кратности 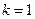. Поэтому решение следует искать в виде

.

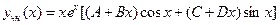3) Пусть правая часть неоднородного ЛДУ представляет сбой сумму числа функции, т.е. .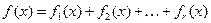

Для наглядности рассмотрим, когда правая часть сумма двух функций

.

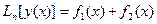Будем решение искать в виде .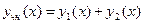

Тогда, подставляя его в уравнение и пользуясь свойством линейного дифференциального оператора, получим

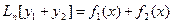или .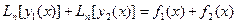

Таким образом, если правая часть уравнения представляет собой сумму 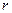функций, то уравнение разбивается на 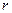уравнений с этими новыми правыми частями. Найдя частное решение каждого неоднородного уравнения, получим частное решение исходного уравнения в виде суммы частных решений этих 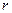уравнений.

3. Заключительная часть:

1.Выводы, итоги занятия.

2.Объявление оценок, замечаний.

3. Задание на самостоятельную подготовку курсантов:

Изучение лекционного материала и дополнительной литературы.