Дифференциальные операции второго порядка.
В результате дифференциальных операций первого порядка мы получаем скалярные и векторные поля 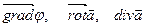 .
.
К ним вновь можно применить дифференциальные операции первого порядка.
От скалярного поля 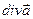 можно взять градиент, получив векторное поле
можно взять градиент, получив векторное поле 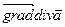 .
.
От векторных полей 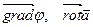 можно взять ротор и дивергенцию, получив скалярные поля
можно взять ротор и дивергенцию, получив скалярные поля 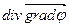 ,
, 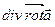 и векторные поля
и векторные поля 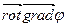 ,
, 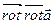 .
.
Итак, дифференциальные операции второго порядка позволяют получить скалярные поля 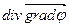 ,
, 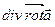 и векторные поля
и векторные поля 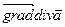 ,
, 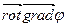 ,
, 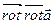 .
.
Ранее было показано, что потенциальное поле – безвихревое, т.е. 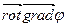 =0.
=0.
Покажем, что поле ротора – соленоидальное поле, т.е. 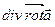 =0.
=0.
Доказательство.
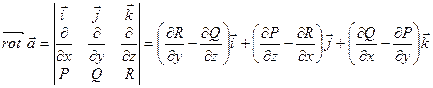
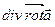 =
= 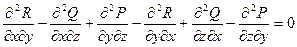 .
.
Три остальных векторных поля связаны друг с другом. Это становится ясным, если рассматривать векторные операции с оператором Гамильтона «набла» аналогично обычным векторным операциям. Однако, эти аналогии не совсем верны, см. подробнее о свойствах оператора «набла» выпуск 7 учебника.
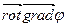 =
= 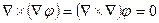 ,
, 
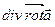 =
= 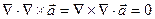
Известно соотношение 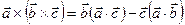 . Перенося это правила на действия с оператором «набла», получим
. Перенося это правила на действия с оператором «набла», получим
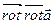
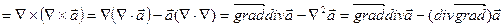 .
.
Здесь 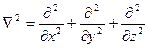 - оператор Лапласа (скаляр – оператор).
- оператор Лапласа (скаляр – оператор).
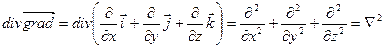 .
.
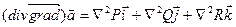 - произведение скаляр-оператора Лапласа на вектор
- произведение скаляр-оператора Лапласа на вектор 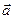 .
.
Дата добавления: 2017-11-21; просмотров: 1666;











