Дифференциальные уравнения первого порядка.

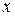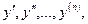Определение.Дифференциальным уравнениемназывается уравнение, связывающее независимую переменную , искомую функцию и ее производные т.е. уравнения вида

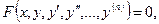(1)
где 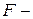непрерывная функция 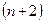переменных.

Если искомая функция есть функция одной независимой переменной, то дифференциальное уравнение называется обыкновенным.

Например,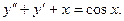

Если искомая функция зависит от нескольких независимых переменных, то дифференциальное уравнение называется уравнением в частных производных.

Например,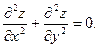

В дальнейшем будем рассматривать лишь обыкновенные дифференциальные уравнения.

Порядком дифференциального уравнения называется порядок наивысшей производной, явно входящей в уравнение.

Например: 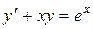- дифференциальное уравнение 1- го порядка;

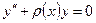- дифференциальное уравнение 2- го порядка;

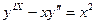- уравнение 9- го порядка.

Решением дифференциального уравнения (1) называется функция 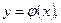которая при подстановке в дифференциальное уравнение обращает его в тождество.

Например, 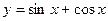является решением дифференциального уравнения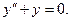

В самом деле,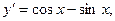

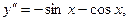
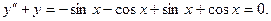
Процесс отыскания решений дифференциального уравнения называется интегрированием уравнения.График решения дифференциального уравнения называется интегральной кривойэтого уравнения.

Дифференциальные уравнения первого порядка

Общий вид уравнения первого порядка следующий:

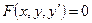(2)
Если уравнение (2) удается разрешить относительно 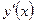, то получим

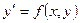(3)
Это уравнение называется уравнением первого порядка,разрешенным относительно производной.