Линейные дифференциальные уравнения второго порядка.

Уравнение вида 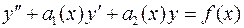. (1)

называется линейным дифференциальным уравнением второго порядка.

Уравнение вида 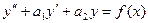(2) называется линейным дифференциальным уравнением с постоянными коэффициентами

Алгоритм решения.

1. Определяем общее решение 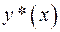соответствующего однородного уравнения .

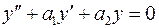2. Подбираем частное решение линейного уравнения (2) 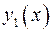(см. таблицу). Если правая часть уравнения состоит из суммы двух функций специального вида, то частное решение искать в виде 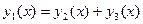. Если правая часть не принадлежит к функциям «специального вида», то подобрать вид частного решения по виду правой части и корням характеристического уравнения нельзя. В данном случае применяется метод вариации произвольных постоянных.

3. Общее решение (2) получается путем сложения по формуле .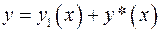

Таблица.

Правая часть дифференциального уравнения	Корни характеристического уравнения	Вид частного решения
f(x) = P_m (x), где P_m (x) – многочлен степени m.	а) Число 0 не является корнем характеристического уравнения.	Q_m (x), где Q_m (x) – многочлен степени не выше m.
б) Число 0 является корнем характеристического уравнения кратности k.	x^kQ_m(x)
f(x) = e^αx P_m (x), где α-вещественное число.	а) Число α не является корнем характеристического уравнения.	Q_m (x)e^αx
б) Число α является корнем характеристического уравнения кратности k.	x^k Qm (x)e^αx
f(x)=P_m(x)cosβx+Q_m(x)sinβx, где P_m(x) и Q_m(x) – многочлены степени не выше m и хоть один из них имеет степень m.	а) Число βi не является корнем характеристического уравнения.	u_m(x)cosβx+v_m(x)sinβx, где u_m(x) и v_m(x) – многочлены степени не выше m.
б) Число βi является корнем характеристического уравнения кратности k.	x^k (u_m(x)cosβx+v_m(x)sinβx)
f(x)= e^αx (P_m(x)cosβx+Q_m(x)sinβx)	а) Число α+βi не является корнем характеристического уравнения.	e^αx (u_m(x)cosβx+v_m(x)sinβx)
б) Число α+βi является корнем характеристического уравнения кратности k.	x^k e^αx (u_m(x)cosβx+v_m(x)sinβx)

Примеры: 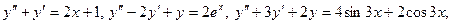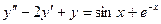- линейные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Дата добавления: 2017-03-12; просмотров: 1286;

Линейные дифференциальные уравнения второго порядка.

Публикации по технике и механике

Публикации по биологии

Публикации по информатике

Публикации по строительству

Публикации по физике

Публикации по химии

Публикации по электронике

Публикации по искусству

Публикации по истории

Публикации по медицине

Публикации по педагогике