Общий интеграл его есть

.

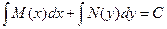Уравнение вида

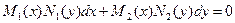, (6)
в которых коэффициенты при дифференциалах распадаются на множители, зависящие только от 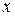и только от 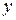, называется уравнением с разделяющимися переменными.

Путем деления обеих частей на произведение 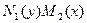они приводятся к уравнениям с разделенными переменными:

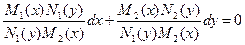
или

,

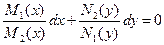т.е. к уравнению вида (5). Общий интеграл этого уравнения имеет вид

.

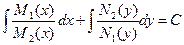Определение 1. Функция 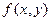называется однородной функцией 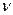-го измерения относительно переменных 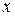и 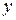, если при любом 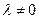справедливо тождество

.

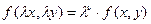
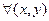Пример:

1) ;

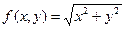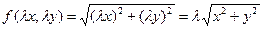
- однородная функция первого измерения.

2) ;

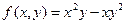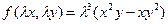
- однородная функция третьего измерения.

3) ;

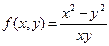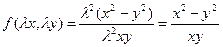
- однородная функция нулевого измерения.

Определение 2.Уравнение первого порядка

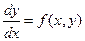(7)
называется однородным уравнением, если функция 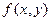есть однородная функция нулевого измерения относительно 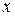и .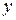

Метод решения однородного уравнения следующий. По условию 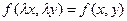. Положим в этом тождестве 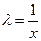, получим 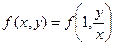, т.е. однородная функция нулевого измерения зависит только от отношения аргументов.

Уравнение (7) в этом случае примет вид

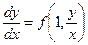(8)
Сделаем подстановку 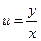, т.е. 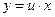. Тогда будем иметь

.

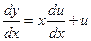Подставляя это выражение производной в уравнение (8) получим

.

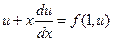Это уравнение с разделяющимися переменными:

, .

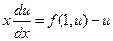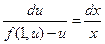Интегрируя, найдем

.

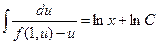Подставляя после интегрирования вместо 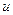отношение 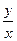, получим интеграл уравнения (8).

Замечание. Уравнение вида 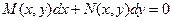будет однородным в том и только в том случае, когда 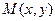и 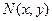являются однородными функциями одного и того же измерения. Это вытекает из того, что отношение двух однородных функций – функций одного и того же измерения является однородной функцией нулевого измерения.

Определение. Линейным уравнением первого порядка называется уравнение, линейное относительно неизвестной функции и ее производной вида

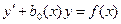, (9)
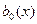где и 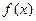- непрерывные функции от .

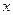Будем искать решение уравнение (9) в виде произведения двух функций от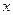

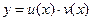. (10)
Дифференцируя обе части равенства (10), находим

.

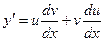Подставляя полученное значение производной 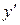в уравнение (9), имеем

,

или

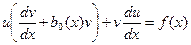. (11)
Выберем функцию 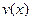такой, чтобы

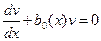(12)
Разделяя переменные в этом дифференциальном уравнении, находим

, .

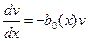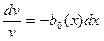Интегрируя, получим

,

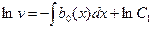или

.

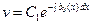Так как нам достаточно какого-нибудь отличного нуля решения уравнения (12), то за функцию 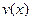возьмем

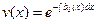. (13)
Очевидно, что .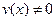

Подставляя найденное значение 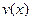в (11) и, учитывая (12), получим

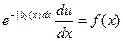
или ; .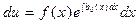

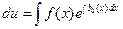
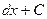Подставляя значения 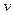и 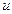в формулу (10), получаем

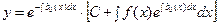. (14)